已知向量
(1)若 ,求
,求 的值;
的值;
(2)记 ,
, 在
在 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是 ,且满
,且满 ,求
,求 的取值范围。
的取值范围。
(本小题满分9分)等比数列 的各项均为正数,且
的各项均为正数,且
(1)求数列 的通项公式;
的通项公式;
(2)设  求数列
求数列 的前n项和.
的前n项和.
(本小题满分9分)若x,y满足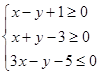 ,求:
,求:
(1)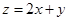 的最小值;
的最小值;
(2)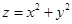 的范围.
的范围.
(3)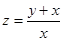 的最大值;
的最大值;
(本小题满分8分)已知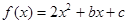 ,不等式
,不等式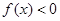 的解集是
的解集是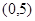 ,
,
(1)求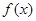 的解析式;
的解析式;
(2)若对于任意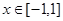 ,不等式
,不等式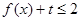 恒成立,求
恒成立,求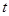 的取值范围.
的取值范围.
(本小题满分7分)在△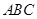 中,角
中,角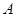 、
、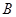 、
、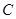 的对边分别为
的对边分别为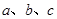 ,若
,若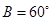 ,且
,且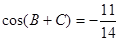 .
.
(1)求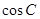 的值;
的值;
(2)若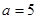 ,求△
,求△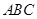 的面积.
的面积.
(本小题满分10分)如图,已知△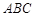 是边长为4的正三角形,
是边长为4的正三角形,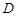 是
是 的中点,
的中点,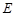 ,
,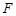 分别是边
分别是边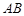 ,
,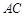 上的点,且
上的点,且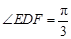 ,设
,设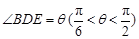 .
.
(Ⅰ)试将线段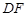 的长表示为
的长表示为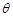 的函数;
的函数;
(Ⅱ)设△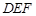 的面积为
的面积为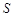 ,求
,求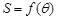 的解析式,并求
的解析式,并求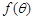 的最小值;
的最小值;
(Ⅲ)若将折线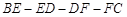 绕直线
绕直线 旋转一周得到空间几何体,试问:该几何体的体积是否有最小值?若有,求出它的最小值;若没有,请说明理由.
旋转一周得到空间几何体,试问:该几何体的体积是否有最小值?若有,求出它的最小值;若没有,请说明理由.