(本题满分14分).如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,
∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=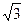 .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点,判定H点位于平面ABCD的那个具体位置?(无须证明)
(Ⅲ)求二面角A-BE-P的大小. 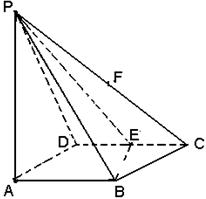
(本小题满分12分)
设 ,点P(
,点P( ,0)是函数
,0)是函数 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(1)用 表示a,b,c;
表示a,b,c;
(2)若函数 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求 的取值范围.
的取值范围.
(本小题满分12分)
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比,比例系数为 ,设AB=2x,BC=y.
,设AB=2x,BC=y.
(1)写出y关于x函数表达式,并指出x的取值范围;
(2)求当x取何值时,凹槽的强度最大.
已知函数 ,且方程
,且方程 有两个实根
有两个实根 .
.
(1)求函数 的解析式;
的解析式;
(2)设 ,解关于
,解关于 的不等式
的不等式
(本小题满分13分)
已知椭圆的中点在原点O,焦点在x轴上,点 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且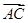 ·
· ="0," |
="0," |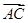 |=|
|=| |.(点C在x轴上方)
|.(点C在x轴上方)
(I)求椭圆的方程;
(II)若平行于CO的直线 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
设函数 .
.
(Ⅰ)求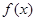 的最小值
的最小值 ;
;
(Ⅱ)若 对
对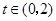 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.