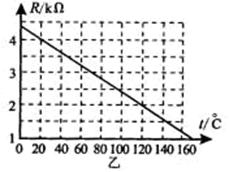
在图甲中,电源的电动势E=9.0V,电源内电阻可忽略不计;G为小量程的电流表,电流表内阻Rg保持不变,R为热敏电阻,其电阻值与温度的变化关系如图乙的R-t图线所示。闭合开关S,当R的温度等于20oC时,电流表示数I1=2mA,则当电流表的示数I2=3.6mA时,热敏电阻R的温度为多少?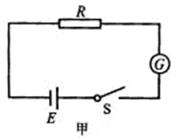
在竖直的井底,将一物块以11 m/s的速度竖直地向上抛出,物块冲过井口时被人接住,在被人接住前1 s内物块的位移是4 m,位移方向向上,不计空气阻力,g取10 m/s2,求:
(1)物块从抛出到被人接住所经历的时间;
(2)此竖直井的深度.
如图所示,水平地面上一个质量M=4.0kg、长度L=2.0m的木板,在F="8.0" N的水平拉力作用下,以v0=2.0m/s的速度向右做匀速直线运动.某时刻将质量m="1.0" kg的物块(物块可视为质点)轻放在木板最右端.(g取10m/s2)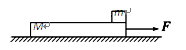
(1)若物块与木板间无摩擦,求物块离开木板所需的时间;
(2)若物块与木板间有摩擦,且物块与木板间的动摩擦因数和木板与地面间的动摩擦因数相等,求将物块放在木板上后,经过多长时间木板停止运动.
如图所示,长为L的细绳上端系一质量不计的环,环套在光滑水平杆上,在细绳的下端吊一个质量为m的铁球(可视作质点),球离地的高度h=L.现让环与球一起以v=的速度向右运动,在A处环被挡住而立即停止,已知A离右墙的水平距离也为L,当地的重力加速度为g,不计空气阻力.求: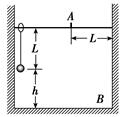
(1)在环被挡住而立即停止时绳对小球的拉力大小;
(2)若在环被挡住后,细绳突然断裂,则在以后的运动过程中,球的第一次碰撞点离墙角B点的距离是多少?
“太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图甲所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时小球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高,圆的半径为R.已知小球的重力为1 N,不计平板的重力,且在A处板对小球的作用力为F.
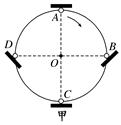
(1)设小球在A处的速度大小为v,写出在A处板对小球的作用力与小球速度大小的关系式;
(2)求在C处板对小球的作用力比在A处大多少?
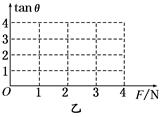
(3)当球运动到B、D位置时,板与水平方向需有一定的夹角θ,才能使小球在竖直面内做匀速圆周运动,请作出tan θ-F的关系图象.
质量m=1.5kg的物体,在水平恒力F=15N的作用下,从静止开始运动0.5s后撤去该力,物体继续滑行一段时间后停下来.已知物体与水平面的动摩擦因数为μ=0.2,g取10m/s2.求:
(1)恒力作用于物体时的加速度大小;
(2)撤去恒力后物体继续滑行的时间;
(3)物体从开始运动到停下来的总位移大小.