如图所示，某货场而将质量为m1="100" kg的货物（可视为质点）从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物从轨道顶端无初速滑下，设货物滑到底端即在A最左端时货物的速度V0=6m/s。地面上紧靠轨道次排放两个完全相同的木板A、B，长度均为l=2m，质量均为m2="100" kg，木板上表面与轨道末端相切。货物与木板间的动摩擦因数为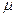
1，木板与地面间的动摩擦因数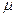=0.2。（最大静摩擦力与滑动摩擦力大小相等，取g="10" m/s2）
①若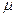1=0.5，且货物滑上木板A时，木板不动，求货物滑到木板A末端时的速度和在木板A上运动的时间。
②若要使货物滑上木板A时，木板不动，而滑上木板B时，木板B开始滑动，求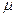1应满足的条件。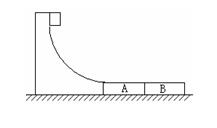
如图所示，一小球从倾角θ为37º的足够长的斜面顶端作平抛运动，初速度为8m/s，A点是小球离斜面最远点。（1）求小球从抛出到再次落到斜面上的时间？（2）求A点离斜面的距离？（3）将A点前后足够小的一段轨迹视为圆弧，求这段圆弧的半径（曲率半径）及小球在A点的向心加速度（法向加速度）与切向加速度？（第三问仅实验班的同学做，不计入总分）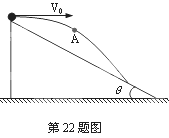
．如图所示，质量为1kg的物体放于倾角θ为37º的足够长的固定斜面底端，受到30N的水平拉力作用而由静止开始向上运动，物体与斜面的动摩擦因数为0.5，2s后将水平拉力撤去（1）求物体向上运动的最高点的位置？（2）水平拉力撤去后还要经过多少时间物体再次回到斜面底端？（3）定性画出物体在斜面上运动全过程的速度——时间图线，以沿斜面向上为速度正方向(不要求说明理由)。
将金属块m用压缩的轻弹簧卡在一个矩形的箱中，如图所示，在箱的上顶板和下底板装有压力传感器，箱可以沿竖直轨道运动，金属块始终没有离开上顶板。当箱以a="2.0" m/s2的加速度竖直向上做匀减速运动时，上顶板的压力显示压力为6.0 N，下底板的压力传感器显示的压力为10.0 N。（g="10" m/s2）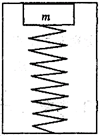
（1）金属块的重力多大?
（2）若上顶板压力传感器的示数是下底板压力传感器的示数的0.4倍，试求箱的加速度大小和方向。
（3）要使上顶板压力传感器的示数为零，箱沿竖直方向运动的情况可能是怎样的?
某物体沿倾角为37°的固定斜面可以匀速下滑，将此斜面倾角增大到53°，让该物体以5 m/s的初速度冲上斜面，则（g=10m/s2，sin53°=0.8，cos53°=0.6）：
（1）物体与斜面间的摩擦因数是多少?
（2）它上滑的最大距离是多大?
如图所示，三条轻绳共同连结于O点，A、B固定在天花板上，另一条绳下端挂一重200 N的物块，处于静止状态。绳的方向如图所示。求OA、OB两绳的拉力分别为多少? 