(本小题满分14分)如图,在直三棱柱ABC—A1B1C1中,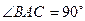 ,
,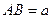 ,
, ,
,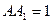 ,点D在棱
,点D在棱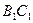 上,且
上,且 ∶
∶ ∶3
∶3
(1)证明:无论a为任何正数,均有BD⊥A1C;
(2)当a为何值时,二面角B—A1D—B1为60°?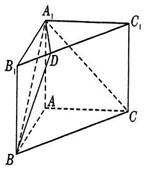
已知函数f(x)=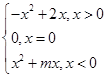 是奇函数.
是奇函数.
(1)求实数m的值;
(2)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围.
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),
当0≤x≤1时,f(x)=x.
(1)求f(3)的值;
(2)当-4≤x≤4时,求f(x)的图像与x轴所围成图形的面积.
已知定义在区间(0,+∞)上的函数f(x)满足f =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,求f(x)在[2,9]上的最小值.
已知f(x)=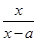 (x≠a).
(x≠a).
(1)若a=-2,试证明f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
规定[t]为不超过t的最大整数,例如[12.6]=12,[-3.5]=-4,对任意实数x,令f1(x)=[4x],g(x)=4x-[4x],进一步令f2(x)=f1[g(x)].
(1)若x=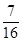 ,分别求f1(x)和f2(x);
,分别求f1(x)和f2(x);
(2)若f1(x)=1,f2(x)=3同时满足,求x的取值范围.