在竖直悬挂的轻质弹簧下端挂一个钩码,弹簧伸长了4cm,如果在该弹簧下端挂两个这样的钩码(弹簧始终发生弹性形变),弹簧的伸长量为
| A.4cm | B.6cm | C.8cm | D.16cm |
.如图所示是汽车中的速度计,某同学在汽车中观察速度计指针位置的变化.开始时指针指示在如图A所示的位置,经过7s后指针指示在如图B所示位置,若汽车做匀变速直线运动,那么它的加速度约为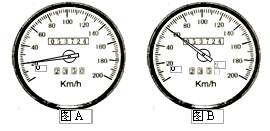
| A.1.6m/s2 |
| B.2.6 m/s2 |
| C.5.7 m/s2 |
| D.7. l m/s2 |
如图所示,用力F把物体紧压在墙上不动,当F增大时,关于墙对物体
的压力F1和摩擦力F2,下列说法正确的是
| A.F1增大,F2减小 | B.F1增大,F2增大 |
| C.F1减小,F2不变 | D.F1增大,F2不变 |
关于物体的重力和重心,下列说法正确的是
| A.形状规则的物体的重心,一定在它的几何中心上 |
| B.物体受到的重力就是地球对物体的吸引力 |
| C.物体的重心位置跟物体的质量分布和几何形状有关 |
| D.形状不规则的物体,总可用悬挂法来确定它的重心位置 |
关于弹力和摩擦力,下列说法正确的是
| A.有弹力必定有摩擦力,有摩擦力必定有弹力。 |
| B.减小物体间的弹力,可以减小物体所受的最大静摩擦力 |
| C.减小物体间的弹力,不影响物体在支持面上滑动时受到的摩擦力 |
| D.滑动摩擦力的方向总是与运动方向相反,起阻碍物体运动的作用 |
下列情况中的物体,哪个可以看作质点
| A.研究一列火车通过某一路标的时间 |
| B.研究正在做课间操的同学们 |
| C.研究原子的内部结构时的原子 |
| D.研究运行中的人造卫星的公转轨迹时的人造卫星 |