(本题14分)数列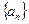 的各项均为正数,
的各项均为正数,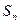 为其前
为其前 项和,对于任意
项和,对于任意 总有
总有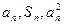 成等差数列。
成等差数列。
(1)求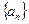 的通项公式;
的通项公式;
(2)设数列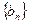 的前
的前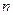 项和为
项和为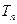 ,且
,且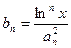 ,求证对任意的实数
,求证对任意的实数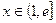 和任意的整数
和任意的整数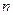 总有
总有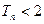 ;
;
(3)正数数列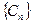 中,
中,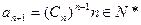 ,求数列
,求数列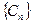 的最大项。
的最大项。
在平面直角坐标系xOy中,△ABC的顶点B、C的坐标为B(-2,0),C(2,0),直线AB,AC的斜率乘积为 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.
(1)求曲线E的方程;
(2)设曲线E与y轴负半轴的交点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与曲线E的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,试求 的取值范围.
的取值范围.
在平面直角坐标系xOy中,曲线y=x2-2x-3与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若直线x+y+a=0与圆C交于A,B两点,且AB=2,求实数a的值.
如图,四棱锥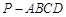 的底面
的底面 是直角梯形,
是直角梯形,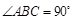 ,
, ,且
,且 ,顶点
,顶点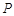 在底面
在底面 内的射影恰好落在
内的射影恰好落在 的中点
的中点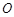 上.
上.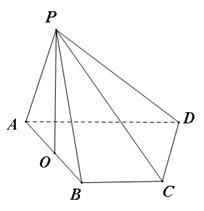
(1)求证: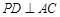 ;
;
(2)若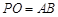 ,求直线
,求直线 与
与 所成角的 余弦值;
所成角的 余弦值;
(3)若平面 与平面
与平面 所成的二面角为
所成的二面角为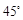 ,求
,求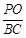 的值.
的值.
已知圆 .
.
(1)若直线 过点
过点 ,且与圆
,且与圆 相切,求直线
相切,求直线 的方程;
的方程;
(2)若圆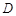 的半径为4,圆心
的半径为4,圆心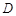 在直线
在直线 :
: 上,且与圆
上,且与圆 内切,求圆
内切,求圆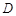 的方程.
的方程.
如图,斜四棱柱 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 ,
,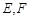 分别为
分别为 的中点.
的中点.
求证:(1)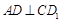 ;(2)
;(2) ∥平面
∥平面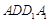 .
.