如图所示，M、N为两块水平放置的平行金属板，板长为L，两板间距也为L，板间电压恒定。今有一带负电粒子（重力不计）以一定的初速度沿两板正中间垂直进入电场，最后打在距板右端为L的竖直屏上。粒子落点距O点的距离为L/2。若大量的上述粒子（与原来的初速度一样，并忽略粒子间相互作用力）从两板间不同的位置垂直进入电场。试求这些粒子落在竖直屏上的范围并在图中画出。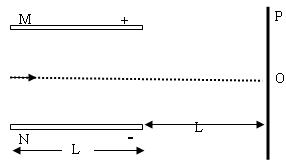
图13（甲）为小型旋转电枢式交流发电机的原理图，其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动，线圈的匝数n=100、电阻r="10" Ω，线圈的两端经集流环与电阻R连接，电阻R="90" Ω，与R并联的交流电压表为理想电表．在t=0时刻，线圈平面与磁场方向平行，穿过每匝线圈的磁通量φ随时间t按图（乙）所示正弦规律变化．求：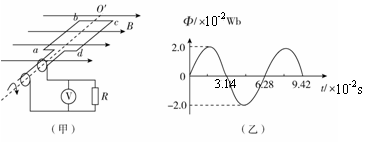
（1）交流发电机产生的电动势最大值；
（2）电路中交流电压表的示数。
如图12为一列简谐横波在t1=0时刻的波形图象，此时波中质点M正处于平衡位置，运动方向沿y轴负方向，到t2=0.55s时质点M恰好第三次到达y轴正方向最大位移处. 试求：
（1）该波传播方向；
（2）该波波速大小。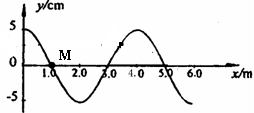 
小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动，当球某次运动到最低点时，绳突然断掉，如图，已知握绳的手离地面高度为d，手与球之间的绳长为3d/4，重力加速度为g，忽略手的运动半径和空气阻力.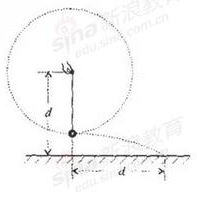
(1)求绳断时球的速度大小V1和球落地时的速度大小V2
(2)求绳能承受的最大拉力多大？
(3)改变绳长，使球重复上述运动，若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？
“嫦娥奔月”的过程可以简化为：“嫦娥一号”升空后，绕地球沿椭圆轨道运动，远地点A距地面高为h1，在远地点时的速度为v，然后经过变轨被月球捕获，再经多次变轨，最终在距离月球表面高为h2="0.5" R2（R2为月球半径）的轨道上绕月球做匀速圆周运动．
(1)．已知地球半径为R1、表面的重力加速度为g0，求“嫦娥一号”沿椭圆轨道运动时在远地点A处的加速度a；(已知万有引力常量为G)
(2)．飞船在距离月球表面高为h2="0.5" R2的轨道上绕行几圈后登陆月球，飞船上备有以下实验器材：
| A．计时表一只（测数据t） | B．弹簧测力计（测数据F） |
| C．已知质量为m的物体一个 | D．天平一只(附砝码一盒) |
已知宇航员在绕行时及着陆后各做了一次测量，依据测量的数据，可求出月球的半径R2及月球的质量M (已知万有引力常量为G)
①两次测量要选用的器材有________________ (用选项符号表示)；
②两次测量的物理量是______________________和____________________；
③试用所给物理量的符号分别写出月球半径R2和质量M的表达式。
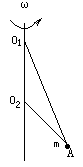
如图：直杆上O1O2两点间距为L,细线O1A长为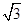
L,O2A长为L,A端小球质量为m，要使两根细线均被拉直，杆应以多大的角速度
转动． 