(本小题8分) 嘉兴市秀洲区为促进淡水鱼养殖业的发展，将价格控制在适当范围内，并决定对淡水鱼养殖提供政府补贴。设淡水鱼的市场价格为
，政府补贴为
。根据市场调查，当
时，淡水鱼的
市场日供应
量
与市场日需求量
近似满足关系：
，
；当
时的市场价格称为市场平衡价格。
（1） 将政府补贴费表示为市场平衡价格的函数，并求出函数的定义域；
（2）为使市场平衡价格不高于
，政府需要补贴吗？如果需要，至少为多少
？
（本小题满分12分）已知函数
，
，且
．
（Ⅰ）若
，求
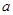的值；
（Ⅱ）当
时，求函数
的最大值；
（本小题满分12分）如图，以原点O为顶点，以y轴为对称轴的抛物线E的焦点为F（0，1），点M是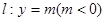
上任意一点，过点M引抛物线E的两条切线分别交x轴于点S，T，切点分别为B，A。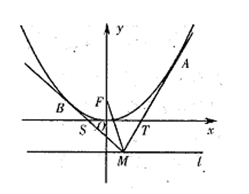
（Ⅰ）求抛物线E的方程；
（Ⅱ）求证：点S，T在以FM为直径的圆上
（本小题满分12分）已知数列
为等差数列，且
．
为等比数列，数列
的前三项依次为3，7，13。求
（1）数列，的通项公式；
（2）数列的前
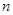项和
。
（本小题满分10分）已知
。
（本小题满分10分）选修4-5：不等式选讲
设不等式
的解集为A，且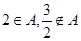
（Ⅰ）求a的值；
（Ⅱ）求函数
的最小值。