定义在R上的偶函数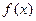 满足
满足 ,且在[-1,0]上单调递增,设
,且在[-1,0]上单调递增,设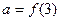 ,
,  ,
,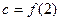 ,则
,则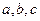 大小关系是( )
大小关系是( )
A. |
B. |
C.  |
D. |
设点G是△ABC的重心,且(56sinA) +(40sinB)
+(40sinB) +(35sinC)
+(35sinC) =0,则角B的大小为( )
=0,则角B的大小为( )
A、450 B、600 C、300 D、150
给出下列三个命题:
①函数 与
与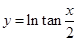 是同一函数;
是同一函数;
②若函数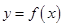 与
与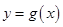 的图像关于直线
的图像关于直线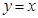 对称,则函数
对称,则函数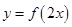 与
与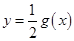 的图像也关于直线
的图像也关于直线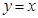 对称;
对称;
③若奇函数 对定义域内任意x都有
对定义域内任意x都有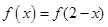 ,则
,则 为周期函数。
为周期函数。
其中真命题是
| A.①② | B.①③ | C.②③ | D.② |
已知函数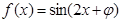 ,其中
,其中 为实数,若
为实数,若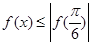 对
对 恒成立,且
恒成立,且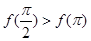 ,则
,则 的单调递增区间是
的单调递增区间是
A. |
B.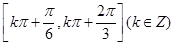 |
C. |
D.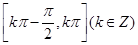 |
函数f(x)=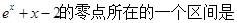
| A.(-2,-1) | B.(-1,0) | C.(1,2) | D.(0,1) |
已知两个单位向量 与
与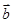 的夹角为
的夹角为 , 若
, 若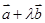 与
与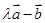 互相垂直,则
互相垂直,则 为( )
为( )
A. 或 或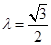 |
B.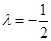 或 或 |
C.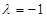 或 或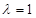 |
D. 为任意实数 为任意实数 |