(本小题满分12分)
已知函数
的图象过坐标原点O,且在点
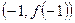处的切线的斜率是
（1）求实数
的值；
（2）求
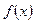在区间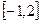
上的最大值；
（3）对任意给定的正实数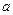
，曲线
上是否存在两点P、Q，使得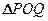
是以O为直角顶点的直角三角形，且此三角形斜边中点在
轴上？说明理由．
已知双曲线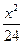
-
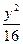=1,P为双曲线上一点，F1、F2是双曲线的两个焦点，并且∠F1PF2=60°，求△F1PF2的面积.
已知曲线C:x2－y2＝１及直线l:y=kx-1.
(1)若l与C有两个不同的交点，求实数k的取值范围；
(2)若l与C交于A、B两点，O是坐标原点，且△AOB的面积为2，求实数k的值.
设A、B是双曲线x2-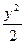
=1的上两点，点N（1，2）是线段AB的中点.（1）求直线AB的方程；（2）如果线段AB的垂直平分线与双曲线相交于C、D两点，那么A、B、C、D四点是否共圆？为什么？
过双曲线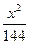
-
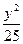=1的一个焦点作x轴的垂线，求垂线与双曲线的交点到两焦点的距离.
求与双曲线16x2-9y2=-144有共同焦点,且过点(0,2)的双曲线的方程.