2009年9月28日温福铁路开行动车组列车，7点47分福州火-优题课

【物理选修3-5】
（1）目前，在居室装修中经常用到花岗岩、大理石等装修材料，这些岩石都不同程度地含有放射性元素，比如，有些含有铀、钍的花岗岩等岩石会释放出放射性惰性气体氡，而氡会发生放射性衰变，放出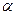、、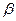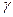射线，这些射线会导致细胞发生癌变及呼吸道等方面的疾病，根据有关放射性知识可知，下列说法正确的是
（）
A．氡的半衰期为3.8天，若取4个氡原子核，经7.6天后就一定剩下一个原子核了
B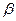．衰变所释放的电子是原子核内的中子转化成质子和电子所产生的
C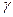．射线一般伴随着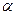或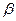射线产生，在这三种射线中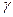，射线的穿透能力最强，电离能力也最强
D．发生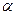衰变时，生成核与原来的原子核相比，中子数减少了4
（2）如图所示，平板小车C静止在光滑的水平面上。现有A、B两个小物体从小车C的两端同时水平地滑上小车，初速度的大小分别为v_A ="1.2" m／s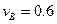，m/s。已知A、B、C三者的质量都相同，A、B与C间的动摩擦因数都是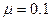，A、B可视为质点。若最后A、B没有相碰，且A、B、C以共同速度运动。求：
①A、B、C共同运动的速度。
②定性描述从A、B滑上小车上以后A、B，C三个物体相对地丽的运动情况。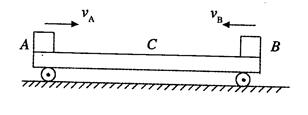

[物理一一选修3-4]（）
（1）以下说法中正确的是

A．横波和纵波都能发生干涉、衍射和偏振现象

B．相对论认为空间和时间与物质的运动状态有关

C．麦克斯韦预言并用实验验证了电磁波的存在

D．在光的双缝干涉实验中，若仅将入射光由绿光变为红光，则条纹间距变窄

（2）一列沿x轴正方向传播的简谐波，在t=0时刻的波的图像如图所示。已知这列波在P出现两次波峰的最短时间是0. 4s，求：
①这列波的波速是多少？
②再经过多长时间R才能第一次到达波峰？这段时间里R通过的路程是多少？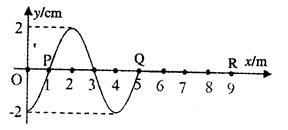

如图所示，在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场，第三象限内有沿y轴负方向的匀强电场，第四象限内无电场和磁场。质量为m、带电量为q的粒子从M点以速度v₀沿x轴负方向进入电场，不计粒子重力的影响，粒子经x轴上的N点和P点最后又回到M点。设OM =L，ON=2L，求：
（1）电场强度E的大小。
（2）匀强磁场的磁感应强度B的大小和方向。
（3）粒子从M点进入电场，经N、P点最后又回到M点所用的总时间。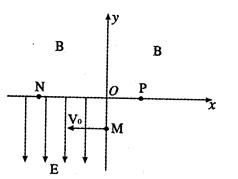

下图是简化后的跳台滑雪的雪道示意图，整个雪道由倾斜的助滑雪道AB和着陆雪道DE，以及水平的起跳平台CD组成，AB与CD圆滑连接。运动员在助滑雪道AB上由静止开始，在重力作用下，滑到D点水平飞出，不计飞行中的空气阻力，经2s在水平方向飞行了60m，落在着陆雪道DE上，已知从B点到D点运动员的速度大小不变，（g=10m／s²），求
（1）运动员在AB段下滑到B点的速度大小；
（2）若不计阻力，运动员在AB段下滑过程中下降的高度。
（3）若运动员的质量为60Kg，在AB段下降的实际高度是50m，其他条件不变，求运动员克服阻力做的功。

[选修3—4](本题共有二小题，第一小题5分，第二小题10分，共15分)
（1）一列简谐横波沿x轴传播，某时刻的波形如图所示.关于波的传播方向与质点a、b、c、d、e的运动情况，下列说法正确的是（）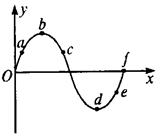

A．若波形沿x轴正方向传播，则质点a运动的速度将减小

B．若质点e比质点d先回到平衡位置，则波沿x轴正方向传播

C．若波形沿x轴负方向传播，则质点c向下运动

D．若波形沿x轴正方向传播，再经过半个周期质点b将运动到质点d现在的位置

（2）如图所示，真空中有一个半径为R=0．1m，质量分布均匀的玻璃球，频率为5．0×10¹⁴Hz的细激光束在真空中沿直线BC传播，于玻璃球表面的C点经折射进入小球，并在玻璃球表面的D点又经折射进人真空中．已知COD=120°，玻璃球对该激光束的折射率为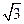，求：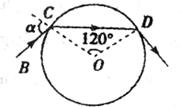

①此激光束在真空中的波长；
②此激光束进入玻璃时的入射角；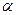

车次	站次	站名	到达时间	开车时间	里程/km
D3102	01	福州南	07:47	07:47	0
D3102	02	宁德	08:16	08:17	88
D3102	03	霞浦	08:36	08:37	147
D3102	04	苍南	09:03	09:04	237
D3102	05	瑞安	09:16	09:17	271
D3102	06	温州南	09:27	09:28	294
D3102	07	台州	10:03	10:04	417
D3102	08	宁海	10:24	10:25	497
D3102	09	宁波	10:53	10:55	569
D3102	10	绍兴	11:54	11:55	677
D3102	11	杭州南	12:21	12:23	713
D3102	12	嘉兴	13:14	13:15	821
D3102	13	上海南	13:58	13:58	901