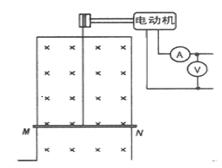
如图所示，左图是游乐场中过山车的实物图片，右图是过山车的原理图。在原理图中半径分别为R1=2．0 m和R2=8．0 m的两个光滑圆形轨道，固定在倾角为α=37°斜轨道面上的Q、Z两点，且两圆形轨道的最高点A、B均与P点平齐，圆形轨道与斜轨道之间圆滑连接。现使小车（视作质点）从P点以一定的初速度沿斜面向下运动。已知斜轨道面与小车间的动摩擦因数为μ=
。问：（已知：g="10" m/s2，sin37°=0．6，cos37°=0．8，
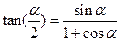。结果可保留根号。）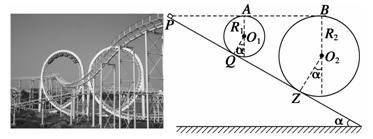
（1）若小车恰好能通过第一个圆形轨道的最高点A处，则其在P点的初速度应为多大?
（2）若小车在P点的初速度为10 m/s，则小车能否安全通过两个圆形轨道?
如图所示，直线MN与水平线夹角为60°，其右侧有一垂直纸面向外的范围足够大的匀强磁场，磁感应强度为Ｂ；直线ＰＱ垂直ＭＮ，且ＰＱ与ＭＮ包围的空间有一匀强电场，电场方向平行于ＰＱ。有一质量为m 电量为+q的带电粒子在纸面内以v0的水平初速度从A点飞入磁场，粒子进入磁场t0(t0未知)时间后立即撤除磁场，此时粒子未到达MN，之后粒子垂直MQ边界从C点（图中未画出）飞入电场；随后粒子再次通过C点。粒子在以上整个过程中所用总时间恰为此带电粒子在磁场中运动一周所需时间，粒子所受重力不计。试求：
（1）粒子在磁场中运动的时间t0
（2）匀强电场场强E的大小。
物块A（可以看成质点）静止在一斜面的底端，斜面倾角a ＝30°，斜面的长为L=1m，物块A与斜面之间的滑动摩擦因数
，斜面固定在水平桌面上。用轻绳跨过斜面顶端的轻滑轮与物块A连接，滑轮与转轴之间的摩擦不计，开始绳刚好绷直，如图所示。若在绳的末端施一竖直向下的恒力F=12N拉绳，物块A由斜面底端到顶端经历的时间为1s。取重力加速度g=10m/s2。
（1）物块A的质量mA是多大？
（2）若物块A静止在斜面底端时，在绳的末端绕过定滑轮挂一质量为1.5kg的物块B由手托住（图中没画出），开始时绳也刚好绷直，则由静止松手后物块A从斜面底端到顶端时B的动能为多少？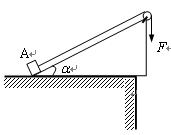
23.如图所示，光滑的圆环半径为R，固定在一粗糙水平面上，水平面与圆环底部相切，跟圆环最低点B相距为L的A处的一质量为m的小球，以v0（未知）速度沿水平轨道进入圆环，并在圆环内做圆周运动，小球与水平间的滑动摩擦因数为μ。问v0应满足什么条件，才能使小球在圆环内做完整的圆周运动？
图为利用高频交变电流焊接金属工件的原理示意图，图中A是高频交流线圈，C是工件，a是工件上的待焊接缝。当线圈A中通入高频电流时，会产生一个交变磁场。假设焊接时，工件C内磁场分布均匀，方向垂直于C所在平面，该磁场在C中产生的感应电动势可视为变化率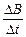
= k的均匀变化磁场所产生的电动势。已知C所围面积为S，焊接时a处的电阻为R，工件其余部分电阻r。求：
(1)焊接时工件中产生的感应电动势E；
(2)焊接时接缝处产生的热功率P。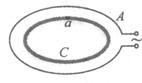
如图，电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升，导体棒的电阻R为1Ω，架在竖直放置的框架上，它们处于磁感应强度B为1T的匀强磁场中，磁场方向与框架平面垂直。当导体棒上升h=3.8m时，获得稳定的速度，导体棒上产生的热量为2J，电动
机牵引棒时，电压表、电流表
的读数一直为7V、1A，电动机内阻r为1Ω，不计框架电阻及一切摩擦，求：
（1）棒能达到的稳定速度；
（2）棒从静止至达到稳定速度所需要
的时间。