正方形金属线框abcd，每边长
=0.1m，总质量m=0.1kg，回路总电阻
Ω，用细线吊住，线的另一端跨过两个定滑轮，挂着一个质量为M=0.14kg的砝码。线框上方为一磁感应强度B=0.5T的匀强磁场区，如图，线框abcd在砝码M的牵引下做加速运动，当线框上边ab进入磁场后立即做匀速运动。接着线框全部进入磁场后又做加速运动（g=10m/s2）。问：
（1）线框匀速上升的速度多大？此时磁场对线框的作用力多大？
（2）线框匀速上升过程中，重物M做功多少？其中有多少转变为电能？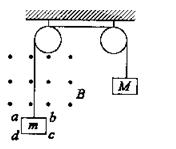
如图甲所示，两块相同的平行金属板M、N正对着放置，相距为
，板M、N上的小孔s1、s2与 O三点共线，s2O=R，连线s1O垂直于板M、N。以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场。收集屏PQ上各点到O点的距离都为2R，两端点P、Q关于连线s1O对称，屏PQ所对的圆心角θ=120°。质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场，接着通过s2进入磁场。质子重力及质子间的相互作用均不计，质子在s1处的速度看作零。
⑴若M、N间的电压UMN=+U时，求质子进入磁场时速度的大小
。
⑵若M、N间接入如图乙所示的随时间t变化的电压
（式中
，周期T已知），且在质子通过板间电场区域的极短时间内板间电场视为恒定，则质子在哪些时刻自s1处进入板间，穿出磁场后均能打到收集屏PQ上？
⑶在上述⑵问的情形下，当M、N间的电压不同时，质子从s1处到打在收集屏PQ上经历的时间t会不同，求t的最大值。
如图，顶角为90°的光滑金属导轨MON固定在水平面上，导轨MO、NO的长度相等，M、N两点间的距离l＝2m，整个装置处于磁感应强度大小B＝0.5T、方向竖直向下的匀强磁场中。一根粗细均匀、单位长度电阻值r＝0.5Ω/m的导体棒在垂直于棒的水平拉力作用下，从MN处以速度v＝2m/s沿导轨向右匀速滑动，导体棒在运动过程中始终与导轨接触良好，不计导轨电阻，求：
⑴导体棒刚开始运动时所受水平拉力F的大小；
⑵开始运动后0.2s内通过导体棒的电荷量q；
⑶导体棒通过整个金属导轨的过程中产生的焦耳热Q。
如图所示，倾角θ=300、长L=2．7m的斜面，底端与一个光滑的1/4圆弧平滑连接，圆弧底端切线水平。一个质量为m=1kg的质点从斜面最高点A沿斜面下滑，经过斜面底端B恰好到达圆弧最高点C，又从圆弧滑回，能上升到斜面上的D点，再由D点由斜面下滑沿圆弧上升，再滑回，这样往复运动，最后停在B点。已知质点与斜面间的动摩擦因数为μ=
/6，g=10m/s2，假设质点经过斜面与圆弧平滑连接处速率不变。求：
（1）质点第1次经过B点时对圆弧轨道的压力
（2）质点从A到D的过程中重力势能的变化量
（3）质点从开始到第8次经过B点的过程中在斜面上通过的路程
如图(a)所示，在水平光滑轨道上停着甲、乙两辆实验小车，甲车系一穿过打点计时器的纸带，当甲车受到水平向右的瞬时冲量时，随即启动打点计时器，甲车运动一段距离后，与静止的乙车发生正碰并粘在一起运动，纸带记录下碰撞前甲车和碰撞后两车运动情况如图（b）所示，电源频率为50Hz，求：甲、乙两车的质量比m甲：m乙
一列向右传播的简谐横波在某时刻的波形图如图所示。波速大小为0.6m/s，P质点的横坐标x = 96cm。求：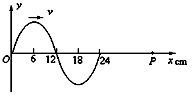
①波源O点刚开始振动时的振动方向和波的周期；
②从图中状态为开始时刻，质点P第一次达到波峰时间。