近地人造卫星1和2绕地球做匀速圆周运动的周期分别为T1和T2,设在卫星1、卫星2各自所在的高度上的重力加速度大小分别为g1、g2,则 ( )
A. |
B. |
C. |
D.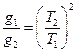 |
(14分)如图10所示,绝缘水平面上静止着两个质量均为m、电荷量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求:
(1)A受的摩擦力为多大?
(2)如果将A的电荷量增至+4Q,两物体开始运动,当它们的加速度第一次为零时,A、B各运动了多远距离?
(12分)如图9所示,两根长均为L的绝缘细线下端各悬挂质量均
为m的带电小球A和B,带电荷量分别为+q和-q,若加上水平向
左的场强为E的匀强电场后,使连接A、B的长也为L的绝缘细线
绷紧,且两球均处于平衡状态.则匀强电场的场强大小E应满足什么条件?
(11分)如图8所示,在竖直放置的光滑半圆弧形绝缘细管的圆心处放一点电荷,将质量为m、带电荷量为q的小球从圆弧管水平直径的端点A由静止释放,当小球沿细管下滑到最低点时,对细管的上壁的压力恰好与球重相同,求圆心处的电荷在圆弧管内产生的电场的场强大小.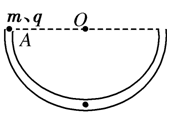
真空中固定的正点电荷Q所形成的电场中有一质量为m=1×10-4 kg、带电荷量q=1×10-8 C的微粒在此点电荷附近以角速度ω=10 rad/s做匀速圆周运动,已知正点电荷Q的带电荷量为4×10-5 C.重力加速度g取10 m/s2,且微粒的重力相对于电场力不能忽略.则下列判断正确的是 ( )
| A.微粒一定带负电 |
| B.微粒一定带正电 |
| C.微粒做圆周运动的圆心就在正点电荷Q所在的位置 |
| D.微粒做圆周运动的圆心就在正点电荷Q正下方与Q的距离为0.1 m的位置 |
如图7所示,在沿水平方向的匀强电场中有a、b两点,已知a、b两点在同一竖直平面内,但不在同一电场线上,一个带电小球在重力和电场力作用下由a点运动到b点,在这一运动过程中,以下判断正确的是 ( )
| A.带电小球的动能可能保持不变 |
| B.带电小球运动的轨迹一定是直线 |
| C.带电小球做的一定是匀变速运动 |
| D.带电小球在a点的速度可能为零 |