已知抛物线 上一点 到其焦点的距离为 .
(Ⅰ)求 p于 m的值;
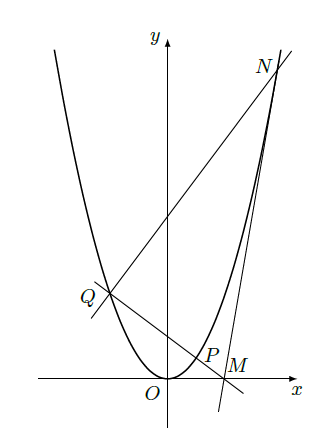
(Ⅱ)设抛物线C上一点 p的横坐标为 t( t>0),过 p的直线交C于另一点 Q,交 x轴于 M点,过点 Q作 PQ的垂线交 C于另一点 N.若 MN是 C的切线,求 t的最小值;
已知函数 .
(Ⅰ)若函数 的图像过原点,且在原点处的切线斜率是-3,求a,b的值;
(Ⅱ)若函数
在区间
上不单调,求a的取值范围. 

设 为数列 的前 n项和, ,其中 是常数.
(Ⅰ)求 及 ;
(Ⅱ)若对于任意的 , , , 成等比数列,求 k的值.
如图, , , , ,P,Q分别为AE,AB的中点.

(Ⅰ)证明: ;
(Ⅱ)求 与 所成角的正弦值.
在 中,角A,B,C所对的边分别为a,b,c,且满足 , .
(Ⅰ)求 的面积;
(Ⅱ)若 ,求 的值.