(本小题满分12分)已知函数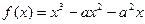 . (Ⅰ)若
. (Ⅰ)若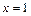 时函数
时函数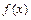 有极值,求
有极值,求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数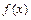 的单调增区间;(Ⅲ)若方程
的单调增区间;(Ⅲ)若方程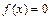 有三个不同的解,分别记为
有三个不同的解,分别记为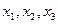 ,证明:
,证明: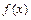 的导函数
的导函数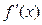 的最小值为
的最小值为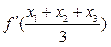 .
.
设不等式2(log x)2+9(log
x)2+9(log x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2
x)+9≤0的解集为M,求当x∈M时函数f(x)=(log2 )(log2
)(log2 )的最大、最小值.
)的最大、最小值.
已知函数x,y满足x≥1,y≥1 loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
已知函数f(x)=logax(a>0且a≠1),(x∈(0,+∞)),若x1,x2∈(0,+∞),判断 [f(x1)+f(x2)]与f(
[f(x1)+f(x2)]与f( )的大小,并加以证明.
)的大小,并加以证明.
设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图像上的点时,点Q(x-2a,-y)是函数y=g(x)图像上的点.
(1)写出函数y=g(x)的解析式;
(2)若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
已知函数f(x)的定义域为R,且对m、n∈R,恒有f(m+n)=f(m)+f(n)-1,且f(-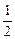 )=0,当x>-
)=0,当x>-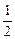 时,f(x)>0.
时,f(x)>0.
(1)求证:f(x)是单调递增函数;
(2)试举出具有这种性质的一个函数,并加以验证.