如图所示，真空室中阴极K逸出电子（初速不计），经过电压为U1的加速电场后，由小孔S沿水平金属极板A、B间的中心线射入,金属极板A、B长均为L，相距为d，两板间加上恒定电压U0，在两极板右侧与极板右端相距D处有一个与两极板中心线垂直的足够大的荧光屏，中心线正好与屏上坐标原点相交．已知电子的质量为me，带电荷量为-e（不计电子的重力）。求：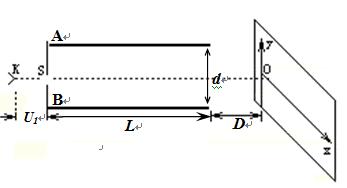
（1）电子刚进入偏转极板A、B时的初速度v=?
（2）要使所有电子都能打在荧光屏上，则所加偏转电压的U0应满足什么条件？
（3）偏转电压满足第2问条件下，求电子从逸出至打到荧光屏上增加的动能。
如图，绝缘的光滑圆弧曲面固定在竖直平面内，B为曲面最低点．曲面上的A点与曲面圆心O的连线与竖直方向成夹角θ=37°．曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场，方向分别是水平向右和竖直向上．开始时有一质量为m的带电小球处于A点恰好保持静止．此后将曲面内的电场撤去，小球沿曲面下滑至B点时以大小为v0的速度水平抛出，最后落在电场内地面的P点，P点与B点间的水平距离为L． 已知tan37°=0.75，重力加速度为g，求：
（1）小球的带电性及电荷量q．
（2）小球运动到P点瞬间的速度vP的大小．
如图甲所示，MN、PQ为间距L="0" .5m足够长的平行导轨，NQ⊥MN，导轨的电阻均不计。导轨平面与水平面间的夹角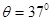
，NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s2。求：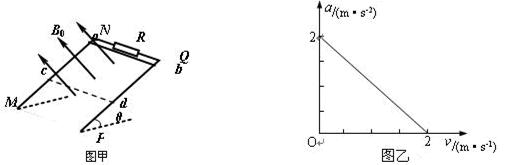
（1）金属棒与导轨间的动摩擦因数μ；
（2）cd离NQ的距离s；
（3）金属棒滑行至cd处的过程中，电阻R上产生的热量；
（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化（写出B与t的关系式）。
如图所示为示波管的示意图，竖直偏转电极的极板长l＝4.0 cm，两板间距离d＝1.0 cm，极板右端与荧光屏的距离L＝18 cm。由阴极发出的电子经电场加速后，以v=1.6×107 m/s沿中心线进入竖直偏转电场。若电子由阴极逸出时的初速度、电子所受重力及电子之间的相互作用力均可忽略不计，已知电子的电荷量e＝1.6×10-19 C，质量m＝0.91×10-30 kg。
（1）求加速电压U0的大小；
（2）要使电子束不打在偏转电极的极板上，求加在竖直偏转电极上的电压应满足的条件；
（3）在竖直偏转电极上加
的交变电压，求电子打在荧光屏上亮线的长度。
如图所示，一质量M=2.0kg的长木板静止放在光滑水平面上，在木板的右端放一质量m=1.0kg可看作质点的小物块，小物块与木板间的动摩擦因数为μ=0.2。用恒力F向右拉动木板使木板在水平面上做匀加速直线运动，经过t=1.0s后撤去该恒力，此时小物块恰好运动到距木板右端l=1.0m处。在此后的运动中小物块没有从木板上掉下来。求：
（1）小物块在加速过程中受到的摩擦力的大小和方向；
（2）作用于木板的恒力F的大小；
（3）木板的长度至少是多少？
如图所示，宽度L=1m的足够长的U形金属框架水平放置，框架处在竖直向上的匀强磁场中，磁感应强度B=1T，框架导轨上放一根质量m=0.2kg、电阻R=1.0Ω的金属棒ab，棒ab与导轨间的动摩擦因数μ=0.5，现用功率恒为6W的牵引力F使棒从静止开始沿导轨运动（ab棒始终与导轨接触良好且垂直）。ab棒从静止开始经过时间t=1.5s获得稳定速度，此过程中，通过棒的电量q=2.8C（框架电阻不计，g取10m/s2）。问：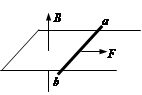
（1）ab棒达到的稳定速度多大？
（2）棒的电阻R产生热量多少？