在半径R="5000" km的某星球表面,宇航员做了如下实验,实验装置如下图甲所示.竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m="0.2" kg的小球,从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H 的大小,可测出相应的F大小,F随H 的变化关系如图乙所示,求:
(1)该星球表面的重力加速度;
(2)该星球的第一宇宙速度.
在排球比赛中,运动员在离地3m处击中排球,使排球以15 m/s的速度水平飞出,若不计空气阻力,g取l0m/s2。 求
(1)排球落地点与击球点之间的水平距离;
(2) 离落地点为2m处的另—个运动员至少用多大的速度跑动,才能在球落地前接到球?
如图所示,足够长的光滑U形导体框架的宽度L =" 0.5" m,电阻忽略不计,其所在平面与水平面成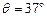 角,磁感应强度B
角,磁感应强度B  =" 0.8" T的匀强磁场方向垂直于导体框平面,一根质量m =" 0.2" kg,有效电阻R = 2Ω的导体棒MN垂直跨放在U形框架上,导体棒由静止开始沿框架下滑到刚开始匀速运动,通过导体棒截面的电量共为Q =" 2" C。求:
=" 0.8" T的匀强磁场方向垂直于导体框平面,一根质量m =" 0.2" kg,有效电阻R = 2Ω的导体棒MN垂直跨放在U形框架上,导体棒由静止开始沿框架下滑到刚开始匀速运动,通过导体棒截面的电量共为Q =" 2" C。求: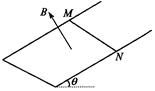
(1)导体棒匀速运动的速度;
(2)导体棒从开始下滑到刚开始匀速运动这一过程中,导体棒的电阻消耗的电功。(sin 37°=" 0.6" cos 37°=" 0.8" g = 10m/s2)
如图所示,一对平行光滑轨 道放置在水平面上,两轨道间距L=1m,电阻R=1.0Ω;有一质量m=1kg的导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻可忽略不计,整个装置处于磁感强度B=0.50T的匀强磁场中,磁场方向垂直轨道面向下.现用一外力F沿轨道方向拉杆,使之以a=
道放置在水平面上,两轨道间距L=1m,电阻R=1.0Ω;有一质量m=1kg的导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻可忽略不计,整个装置处于磁感强度B=0.50T的匀强磁场中,磁场方向垂直轨道面向下.现用一外力F沿轨道方向拉杆,使之以a= 1m/s2的加速度做匀加速运动,速度达5m/s后导体杆做匀速直线运动,通过计算求出外力F与时间t的函数关系,并在下图中画出前10s内的F-t图象.
1m/s2的加速度做匀加速运动,速度达5m/s后导体杆做匀速直线运动,通过计算求出外力F与时间t的函数关系,并在下图中画出前10s内的F-t图象.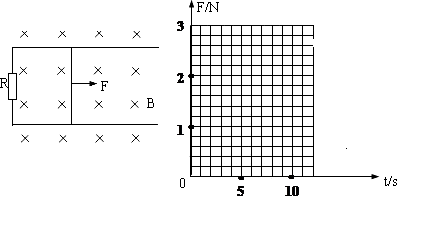
如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成 的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界。线框在水平恒力作用下向右运动,其中ab边保持与MN平行。当线框以速度v0进入磁场区域时,它恰好做匀速运动。在线框进入磁场的过程中,
的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界。线框在水平恒力作用下向右运动,其中ab边保持与MN平行。当线框以速度v0进入磁场区域时,它恰好做匀速运动。在线框进入磁场的过程中, 
(1)线框的ab边产生的感应电动势的大小为E 为多少?
(2)求线框a、b两点的电势差。
(3)求线框中产生的焦耳热。
如图所示,面积为0.2 m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面.已知磁感应强度随时 间变化的规律如图,定值电阻R1="6" Ω,线圈电阻R2="4" Ω,求:
间变化的规律如图,定值电阻R1="6" Ω,线圈电阻R2="4" Ω,求:
(1)在图中标出流过R1的电流方向
(2) 回路中的感应电动势 大小;
大小;