如图为宇宙中有一个恒星系的示意图。A为星系的一颗行星,它绕中央恒星O运行的轨道近似为圆。天文学家观测得到A行星运动的轨道半径为 、周期为
、周期为 。
。
(1)中央恒星O的质量为多大?
(2)经长期观测发现,A行星实际运动的轨道与圆轨道总存在一些偏离,且周期性地每隔时间 发生一次最大的偏离。天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一水平面内,且与A的绕行方向相同),它对A行星的万有引力引起A轨道的偏离。(由于B对A的吸引而使A的周期引起的变化可以忽略)根据上述现象及假设,试求未知行星B的运动周期T及轨道半径R。
发生一次最大的偏离。天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一水平面内,且与A的绕行方向相同),它对A行星的万有引力引起A轨道的偏离。(由于B对A的吸引而使A的周期引起的变化可以忽略)根据上述现象及假设,试求未知行星B的运动周期T及轨道半径R。
图(甲)为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻 r="10" Ω,线圈的两端经集流环与电阻R连接,电阻R="90" Ω,与R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图(乙)所示正弦规律变化.求:
(1)交流发电机产生的电动势最大值;
(2)电路中交流电压表的示数。
如图所示,在水平光滑直导轨上,静止着三个质量均为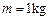 的相同小球
的相同小球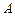 、
、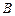 、
、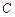 ,现让
,现让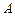 球以
球以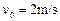 的速度向着
的速度向着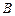 球运动,
球运动,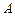 、
、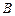 两球碰撞后黏合在一起,两球继续向右运动并跟
两球碰撞后黏合在一起,两球继续向右运动并跟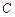 球碰撞,碰后
球碰撞,碰后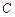 球的速度
球的速度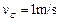 .
.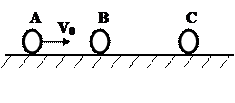
①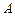 、
、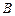 两球跟
两球跟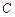 球相碰前的共同速度多大?
球相碰前的共同速度多大?
②两次碰撞过程中一共损失了多少动能?
图示是一透明的圆柱体的横截面,其半径R=20cm,折射率为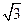 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
①光在圆柱体中的传播速度
②距离直线AB多远的入射光线,折射后恰经过B点
(12分)如图为一列简谐横波在t1=0时刻的波形图象,此时波中质点M正处于平衡位置,运动方向沿y轴负方向,到t2=0.55s时质点M恰好第三次到达y轴正方向最大位移处. 试求:
(1)该波传播方向;
(2)该波波速大小;
(3)从t1=0到t3=1.2s,波中质点N走过的
路程和相对于平衡位置的位移分别是多少?
如图所示,真空中有一沿X轴正方向的匀强电场,一质量为m、电量为q的带电微粒从坐标原点O沿OP方向以速度OP与X轴的夹角是45°。(重力加速度为g)v0射入电场,恰能沿直线OP运动,在A点微粒速度变为零。已知
(1)微粒带什么电?
(2)匀强电场的电场强度E=?
(3)O、A两点之间的电势差UOA=?