双曲线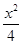 -y2=1的顶点到其渐近线的距离等于()
-y2=1的顶点到其渐近线的距离等于()
A.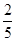 |
B.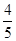 |
C. |
D.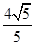 |
椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为()
A.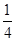 |
B.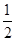 |
C.2 | D.4 |
双曲线方程: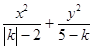 =1,那么k的范围是()
=1,那么k的范围是()
| A.k>5 | B.2<k<5 |
| C.-2<k<2 | D.-2<k<2或k>5 |
(有点难度哦)若a、b、c>0且a(a+b+c)+bc=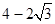 ,则2a+b+c的最小值为()
,则2a+b+c的最小值为()
A.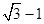 |
B.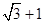 |
C.2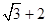 |
D.2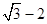 |
不等式组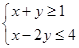 的解集记为D,有下面四个命题:
的解集记为D,有下面四个命题:
p1:∀(x,y)∈D,x+2y≥-2,
p2:∃(x,y)∈D,x+2y≥2,
p3:∀(x,y)∈D,x+2y≤3,
p4:∃(x,y)∈D,x+2y≤-1.
其中的真命题是()
| A.p2,p3 | B.p1,p2 | C.p1,p4 | D.p1,p3 |