(本小题满分12分)已知直线 经过直线
经过直线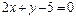 与
与 的交点.
的交点.
(1)若点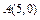 到
到 的距离为3,求
的距离为3,求 的方程;
的方程;
(2)求点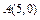 到
到 的距离的最大值,并求此时
的距离的最大值,并求此时 的方程.
的方程.
(本小题满分14分)定义在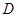 上的函数
上的函数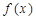 ,如果满足:对任意
,如果满足:对任意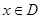 ,存在常数
,存在常数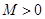 ,都有
,都有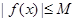 成立,则称
成立,则称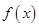 是
是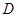 上的有界函数,其中
上的有界函数,其中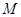 称为函数
称为函数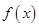 的上界.
的上界.
已知函数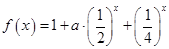 ;
;
(1)当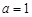 时,求函数
时,求函数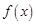 在
在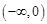 上的值域,并判断函数
上的值域,并判断函数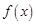 在
在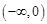 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数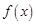 在
在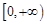 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数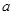 的取值范围
的取值范围
(本小题满分14分)已知函数f(x)=ax+ (a>1).
(a>1).
(1)判定函数f(x)在(-1,+∞)上的单调性,并给出证明;
(2)证明方程f(x)=0没有负数根.
(本小题满分14分)已知函数f(x)=a2x+2ax-1(a>0,且a≠1)在区间[-1,1]上的最大值为14,求实数a的值.
(本小题满分14分) 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0).
(1)求f(x)的解析式
(2)定义函数g(x)=f(x)·(x-1),求函数g(x)的最大值。
(本小题满分12分)已知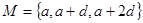 ,
, ,
,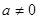 ,M=N,求q的值
,M=N,求q的值