(本小题满分15分)
已知以点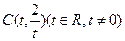 为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点。
(Ⅰ)求证:△AOB的面积为定值;
(Ⅱ)设直线2x+y-4=0与圆C交于点M、N,若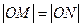 ,求圆C的方程;
,求圆C的方程;
(Ⅲ)在(Ⅱ)的条件下,设P、Q分别是直线l:x+y+2=0和圆C的动点,求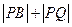 的最小值及此时点P的坐标。
的最小值及此时点P的坐标。
已知函数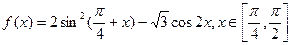 。
。
(1)求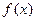 的最大值与最小值。
的最大值与最小值。
(2)若不等式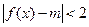 在
在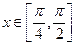 恒成立,求实数
恒成立,求实数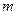 的取值范围
的取值范围
20.等比数列{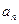 }的前n项和为
}的前n项和为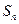 , 已知对任意的
, 已知对任意的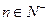 ,点
,点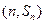 均在函数
均在函数 且
且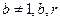 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(2)当b=2时,记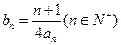 求数列
求数列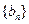 的前
的前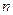 项和
项和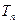
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
(1)求证: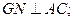
(2)当FG=GD时,在棱AD上确定一点P,使得GP//平面FMC,并给出证明. 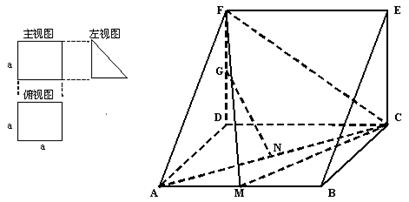
当某电视生产厂家有A、B两种型号的电视机参加家电下乡活动。若厂家投放A、B 型号电视机的价值分别为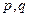 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为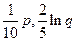 万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到
万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到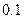 ,参考数据:
,参考数据: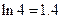 )
)
在直角三角形ABC中,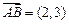 ,
,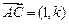 ,求实数
,求实数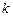 的值.
的值.