如图所示，水平放置的平行板电容器与一恒定的直流电源相连，两极板间距离d=10cm。距下板4cm处有质量m=0.01g的不带电小球由静止落下。小球和下极板碰撞间带上了q=1.0×10-8C的电荷，反跳的高度为8cm，这时下板所带电荷量为Q=1.0×10-6C。如果小球和下板碰撞时没有机械能损失，（取g=10m/s2）试求：
（1）该电容器极板间的电场强度多大？
（2）该电容器的电容多大？
小球在外力作用下，由静止开始从A点出发做匀加速直线运动，到B点时消除外力．然后，小球冲上竖直平面内半径为R的光滑半圆环，恰能维持在圆环做圆周运动，到达最高点C后抛出，最后落回到原来的出发点A处，如图所示，试求小球在AB段运动的加速度为多大?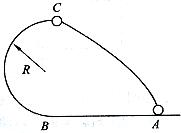
如图所示，质量m=60kg的高山滑雪运动员，从A点由静止开始沿滑雪道滑下并从B点水平飞出，最后落在雪道上的C处。已知AB两点间的高度差为h=25m，BC段雪道与水平面间倾角θ=37°，B、C两点间的距离为x=75m，
，取g=10m/s2
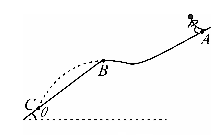
求：
（1）运动员从B点水平飞出时的速度大小；
（2）运动员从A点到B点的过程中克服阻力做的功。
如图所示为一列简谐横波在t=0时刻的图象。此时质点P的运动方向沿y轴负方向，且当t=0.55s时质点P恰好第3次到达y轴正方向最大位移处。问：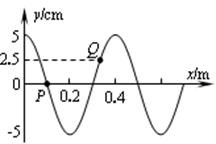
（1）该简谐横波的波速v的大小和方向如何？
（2）从t=0至t=1.2s，质点Q运动的路程L是多少？
（3）当t=1.2s时，质点Q相对于平衡位置的位移s的大小是多少？
钍核
发生衰变生成镭核
并放出一个粒子。设该粒子的质量为
、电荷量为q，它进入电势差为U的带窄缝的平行平板电极
和
间电场时，其速度为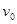
，经电场加速后，沿
方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场，垂直平板电极，当粒子从
点离开磁场时，其速度方向与方位的夹角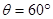
，如图所示，整个装置处于真空中。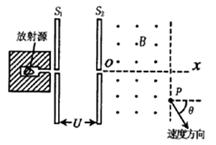
（1）写出钍核衰变方程；
（2）求粒子在磁场中沿圆弧运动的轨道半径R；
（3）求粒子在磁场中运动所用时间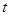
。
核反应堆的工作原理是利用中子轰击重核发生裂变反应，释放出大量核能。核电站就是利用核反应堆释放的核能转化为电能。
（1）核反应方程式
U+01n→
Ba+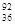
Kr+3 01n 是反应堆中发生的许多核反应中的一种，以mU、m
、
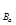分别表示U、Ba、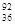Kr核的质量，mn、mp分别表示中子、质子的质量，c为光在真空中传播的速度，求在上述核反应过程中放出的核能△E。
（2）有一座发电能力为P=1.00×106kW的核电站，核能转化为电能的效率η=40%。假定反应堆中发生的裂变反应全是本题（1）中的核反应，已知每次核反应过程放出的核能△E=2.78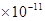
J，U核的质量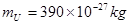
。求每年（1年=3.15×107s）消耗的U的质量。