在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题: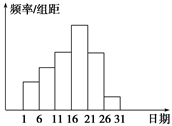
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
(本小题满分14分)已知平行四边形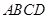 ,
, ,
, ,
, ,
, 为
为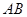 的中点,把三角形
的中点,把三角形 沿
沿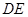 折起至
折起至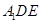 位置,使得
位置,使得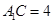 ,
,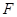 是线段
是线段 的中点.
的中点.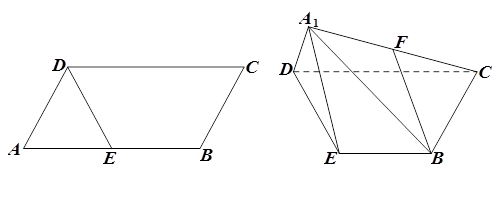
(1)求证: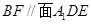 ;
;
(2)求证:面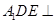 面
面 ;
;
(3)求二面角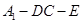 的正切值.
的正切值.
(本小题满分12分)某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
 (月) (月) |
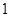 |
 |
 |
 |
 |
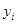 (千克) (千克) |
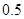 |
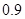 |
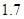 |
 |
 |
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图. 
(2)请根据上表提供的数据,用最小二乘法求出变量 关于变量
关于变量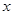 的线性回归直线方程
的线性回归直线方程 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: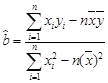 ,
,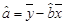 )
)
(本小题满分12分)
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
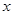 |
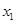 |
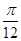 |
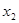 |
 |
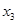 |
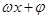 |
 |
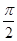 |
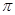 |
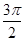 |
 |
 |
1 |
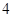 |
1 |
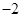 |
1 |
(1)求函数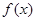 的解析式;
的解析式;
(2)若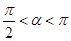 ,
,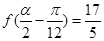 ,求
,求 的值.
的值.
(本小题满分10分)选修4—5:不等式选讲
设关于x的不等式|3x-2|<a (a∈R)的解集为A,且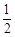 ∈A, -
∈A, - ÏA.
ÏA.
(1)对任意的x∈R, |x+5|+|x+3|≥a2+a恒成立,且a∈N,求a的值;
(2)若点M(a, b)在直线x+y=3上,求 的最小值
的最小值
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l的参数方程为 (t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(1)若|AB|=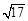 ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P的极坐标为(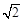 ,
,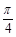 ),且满足2
),且满足2 ,求此时直线l的直角坐标方程.
,求此时直线l的直角坐标方程.