甲、乙两个同学在直跑道上练习4×100m接力跑,如下图所示,他们在奔跑时有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀变速运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑达到最大速度的80%,则: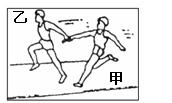
(1)乙在接力区需奔出多少距离?
(2)乙应在距离甲多远时起跑?
利用图(a)实验可粗略测量人吹气产生的压强。两端开口的细玻璃管水平放置,管内塞有潮湿小棉球,实验者从玻璃管的一端
吹气,棉球从另一端
飞出,测得玻璃管内部截面积
,距地面高度
,棉球质量
,开始时的静止位置与管口
的距离
,落地点
与管口
的水平距离
。然后多次改变
,测出对应的
,画出
关系图线,如图(b)所示,并由此得出相应的斜率
。
(1)若不计棉球在空中运动时的空气阻力,根据以上测得的物理量可得,棉球从
端飞出的速度
=。
(2)假设实验者吹气能保持玻璃管内气体压强始终为恒定值,不计棉球与管壁的摩擦,重力加速度
,大气压强
均为已知,利用图(b)中拟合直线的斜率
可得,管内气体压强
=。
(3)考虑到实验时棉球与管壁间有摩擦,则(2)中得到的
与实际压强相比(填偏大、偏小)。
①在“长度的测量”实验中,调整游标卡尺两侧脚间距离,主尺和游标的位置如图所示,此时卡尺两脚间狭缝宽度为_______mm;若要狭缝宽度调到0.20mm,应使游标上除0刻度线外第_______条刻度线与主尺上表示_________mm的刻度线对齐。

②如图所示,螺旋测微器测出的金属丝的直径是__________mm.
气垫导轨(如图甲)工作时,空气从导轨表面的小孔喷出,在导轨表面和滑块内表面之间形成一层薄薄的空气层,使滑块不与导轨表面直接接触,大大减小了滑块运动时的阻力。为了验证动量守恒定律,在水平气垫导轨上放置两个质量均为
的滑块,每个滑块的一端分别与穿过打点计时器的纸带相连,两个打点计时器所用电源的频率均为
.气垫导轨正常工作后,接通两个打点计时器的电源,并让两滑块以不同的速度相向运动,两滑块相碰后粘在一起继续运动。图乙为某次实验打出的、点迹清晰的纸带的一部分,在纸带上以同间距的
个连续点为一段划分纸带,用刻度尺分别量出其长度
、
和
.若题中各物理量的单位均为国际单位,那么,碰撞前两滑块的动量大小分别为、,两滑块的总动量大小为;碰撞后两滑块的总动量大小为。重复上述实验,多做几次。若碰撞前、后两滑块的总动量在实验误差允许的范围内相等,则动量守恒定律得到验证。

在弹性限度内,弹簧弹力的大小与弹簧伸长(或缩短)的长度的比值,叫做弹簧的劲度系数。为了测量一轻弹簧的劲度系数,某同学进行了如下实验设计:如图所示,将两平行金属导轨水平固定在竖直向下的匀强磁场中,金属杆
与导轨接触良好,水平放置的轻弹簧一端固定于
点,另一端与金属杆连接并保持绝缘。在金属杆滑动的过程中,弹簧与金属杆、金属杆与导轨均保持垂直,弹簧的形变始终在弹性限度内,通过减小金属杆与导轨之间的摩擦和在弹簧形变较大时读数等方法,使摩擦对实验结果的影响可忽略不计。
请你按要求帮助该同学解决实验所涉及的两个问题。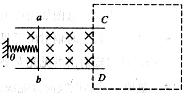
①帮助该同学完成实验设计。请你用低压直流电源( )、滑动变阻器(
)、滑动变阻器( )、电流表(
)、电流表( )、开关(
)、开关( )设计一电路图,画在图中虚线框内,并正确连在导轨的
、
两端。
)设计一电路图,画在图中虚线框内,并正确连在导轨的
、
两端。
②若已知导轨间的距离为
,匀强磁场的磁感应强度为
,正确连接电路后,闭合开关,使金属杆随挡板缓慢移动,当移开挡板且金属杆静止时,测出通过金属杆的电流为
,记下金属杆的位置,断开开关,测出弹簧对应的长度为
1;改变滑动变阻器的阻值,再次让金属杆静止时,测出通过金属杆的电流为
,弹簧对应的长度为
,则弹簧的劲度系数
=.
在通用技术课上,某小组在组装潜艇模型时,需要一枚截面为外方内圆的小螺母,如图所示。现需要精确测量小螺母的内径,可选用的仪器有: A.
等分的游标卡尺 B.螺旋测微器
A.
等分的游标卡尺 B.螺旋测微器 ①在所提供的仪器中应选用。
①在所提供的仪器中应选用。 ②在测量过程中,某同学在小螺母中空部分360°范围内选取不同的位置进行多次测量取平均值的目的是。
②在测量过程中,某同学在小螺母中空部分360°范围内选取不同的位置进行多次测量取平均值的目的是。
