已知函数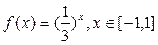 ,函数
,函数
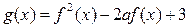 的最小值为
的最小值为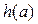 。
。
(1)求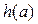 的表达式。
的表达式。
(2)是否存在实数m,n同时满足以下条件:
① m>n>3;
② 当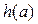 的定义域为[m,n]时,值域为
的定义域为[m,n]时,值域为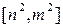
若存在,求出m,n的值;若不存在,说明理由。
((本小题满分13分)
已知三个正数 满足
满足 .
.
(Ⅰ)若 是从
是从 中任取的三个数,求
中任取的三个数,求 能构成三角形三边长的概率;
能构成三角形三边长的概率;
(Ⅱ)若 是从区间
是从区间 内任取的三个数,求
内任取的三个数,求 能构成三角形三边长的概率.
能构成三角形三边长的概率.
((本小题满分12分 )
)
(Ⅰ)用分期付款方式购买家用电器一件,价格为 元,购买当天先付
元,购买当天先付
 元,以后每月这一天都交付
元,以后每月这一天都交付 元,并加付欠款利息,月利率为
元,并加付欠款利息,月利率为 .若交付
.若交付 元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?
元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?
(Ⅱ)用分期付款方式购买家用电器一件,价格为 元,购买当天先付
元,购买当天先付 元,以后每月这一天还款一次,每次还款数额相同,
元,以后每月这一天还款一次,每次还款数额相同,
 个月还清,月利率为
个月还清,月利率为 ,按复利计息.若交付
,按复利计息.若交付 元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有
元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有 效数字)
效数字)
参考数据: ,
, ,
, .
.
((本小题满分12分)
如图所示,正方形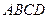 和矩形
和矩形 所在的平面相互垂直,已知
所在的平面相互垂直,已知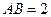 ,
, .
.
(Ⅰ)求证: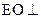 平面
平面 ;
;
(Ⅱ)求二面角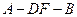 的大小.
的大小.
(本小题满分12分)
某员工参加 项技能测试(技能测试项目的顺序固定),假设该员工在每一项技能测试中获得优秀的概率均为0.9,且不同技能测试是否获得优秀相互独立.该员工所在公司规定:三项均获得优
项技能测试(技能测试项目的顺序固定),假设该员工在每一项技能测试中获得优秀的概率均为0.9,且不同技能测试是否获得优秀相互独立.该员工所在公司规定:三项均获得优 秀则奖励
秀则奖励 千元,有
千元,有 项获得优秀奖励
项获得优秀奖励 千元,一项获得优秀奖励
千元,一项获得优秀奖励 千元,没有项目获得优秀则没有奖励.记
千元,没有项目获得优秀则没有奖励.记 为该员工通过技能测试获得的奖励金(单位:元).
为该员工通过技能测试获得的奖励金(单位:元).
(Ⅰ)求该员工通过技能测试可能获得奖励金 的分布列;
的分布列;
(Ⅱ)求该员工通过技能测试可能 获得的奖励金
获得的奖励金 的均值.
的均值.
(本小题满分12分)
已知向量 ,
, ,若向量
,若向量 与
与 的夹角为
的夹角为 ,且
,且 求
求 的值.
的值.