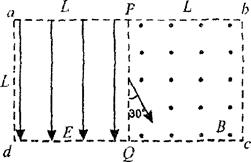
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L＝3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r＝1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为q＝37°。现有一质量为m＝1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ＝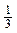
，设小球经过轨道连接处均无能量损失。（g＝10m/s2，sin37°＝0.6，cos37°＝0.8），求：
（1）要使小球完成一周运动回到B点，初动能EK0至少多大？
（2）若以题（1）中求得的最小初动能EK0从B点向上运动，求小球第二次到达D点时的动能；
（3）若以题（1）中求得的最小初动能EK0从B点向上运动，求小球在CD段上运动的总路程。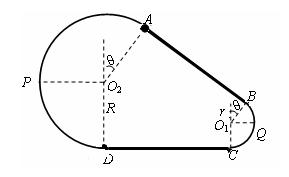
一台交流发电机额定输出功率为P=4.0×103KW,以400V的电压接到升压变压器后向远方输电。若输电线的总电阻为10Ω，允许输电线损失的功率为10﹪，使用得升压变压器、降压变压器都是理想变压器，求：
（1）升压变压器原、副线圈得匝数之比和输出电流。
（2）为了使远方得用户负载能获得得220V工作电压，则降压变压器的原、副线圈得匝数比是多少？实际输送到用户的总功率是多少？
如图所示，MN为裸金属杆，在重力的作用下，贴着竖直平面内的光滑金属长直导轨下滑，导轨的间距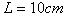
，导轨的上端接有
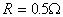的电阻，导轨和金属杆的电阻不计，整个装置处于
的水平匀强磁场中，当杆稳定匀速下落时，每秒有0.02J的重力势能转化为电能，则这时MN杆的下落速度v的大小等于多少？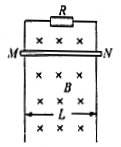
如图位于竖直平面上半径为R的1/4圆弧光滑轨道AB，A点距离地面高度为H，质量为m的小球从A点由静止释放，通过B点对轨道的压力为3mg，最后落在地面C处，不计空气阻力，求：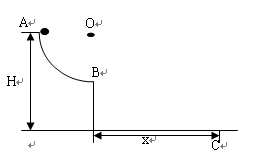
（1）小球通过B点的速度
（2）小球落地点C与B点的水平距离x
如图所示，一个竖直放置的圆锥筒可绕中心轴OO′转动，筒内壁粗糙，筒口半径和筒高分别为R和H，筒内壁A点的高度为筒高的一半。内壁上有一质量为m的小物块。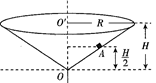
求∶
（1）当筒不转动时，物块静止在筒壁A点受到的摩擦力和支持力的大小；
（2）当物块在A点随筒做匀速转动，且其所受到的摩擦力为零时，筒转动的角速度。
如图所示，虚线框abcd内为边长均为L的正形匀强电场和匀强磁场区域，电场强度的
大小为E，方向向下，磁感应强度为B，方向垂直纸面向外，PQ为其分界线，现有一群质量为m，电荷
量为-e的电子(重力不计)从PQ中点与PQ成300。角以不同的初速射入磁场，求：(1)能从PQ边离开
磁场的电子在磁场运动的时间．
(2)若要电子在磁场运动时间最长，其初速v应满足的条件?
(3)若电子在满足(2)中的条件下且以最大速度进入磁场，最终从电场aP边界飞出虚线框所具有的动能Ek.．