宇宙中存在一些质量相等且离其他恒星
较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用，设每个星体的质量均为m，四颗星稳定地分布在边长为a的正方形的四个顶点上，已知这四颗星均围绕正方形对角线的交点做匀速圆周运动，引力常量为G，试求：星体做匀速圆周运动的周期．
把一个电荷量为q＝5×10－9 C的正电荷从距电场无穷远处移到电场中M点，电荷克服电场力做功WM＝6.0×10－3 J，如果把该点电荷从距电场无穷远处移到电场中N点，电荷克服电场力做功WN＝3.6×10－3 J．取无穷远处为零电势点，求：
(1)M、N点的电势是多少？
(2)M、N点的电势差是多少？把该点电荷从M点移到N点电场力做功是多少？
如图甲所示的螺线管，匝数n＝1500匝，横截面积S＝20cm2，电阻r＝1.5Ω，与螺线管串联的外电阻R1＝3.5Ω，R2＝25Ω，方向向右穿过螺线管的匀强磁场，磁感应强度按图乙所示规律变化，试计算电阻R2的电功率和a、b两点的电势差．
如图所示，光滑绝缘细杆竖直放置，细杆右侧距杆0.3m处有一固定的点电荷Q，A、B是细杆上的两点，点A与Q、点B与Q的连线与杆的夹角均为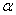
=37°。中间有小孔的带电小球穿在绝缘细杆上滑下，通过A点时加速度为零，取g=10m/s2，求小球下落到B点时的加速度大小。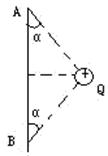
如图，靠正电荷导电的矩形薄片长l=4.0×10-2m，高h=1.0×10-2m；匀强磁场垂直于薄片向外，磁感应强度B=2.0T.若P、Q间通入I=3.0A电流后，M、N间产生稳定的电势差，薄片内正电荷定向移动的平均速率v=5.0×10-4m/s。
（1）求矩形薄片受的安培力大小
（2）判断M、N电势的高低并求出M、N间的电压。
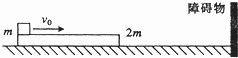
（如图所示，在光滑水平地面上有一质量为2m的长木板，其左端放有一质量为m的重物（可视为质点），重物与长木板之间的动摩擦因数为
。开始时，长木板和重物都静止，现在给重物以初速度v0，设长木板撞到前方固定的障碍物前，长木板和重物的速度已经相等。已知长木板与障碍物发生弹性碰撞，为使重物始终不从长木板上掉下来，求长木板的长度L至少为多少？（重力加速度为g）