滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性。如图所示, 为同一竖直平面内的滑行轨道,其中
为同一竖直平面内的滑行轨道,其中 段水平,
段水平, 、
、 和
和 段均为倾角
段均为倾角 37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略)。已知
37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略)。已知 m,
m, m,
m, m,
m, m,设滑板与
m,设滑板与 轨道之间的摩擦力为它们间
轨道之间的摩擦力为它们间 压力的
压力的 倍(
倍( =0.25),运动员连同滑板的总质量
=0.25),运动员连同滑板的总质量 ="60" kg。运动员从
="60" kg。运动员从 点由静止开始下滑从
点由静止开始下滑从 点水平飞出,在
点水平飞出,在 上着陆后,经短暂的缓冲动作后保留沿斜面方向的分速度下滑,接着在
上着陆后,经短暂的缓冲动作后保留沿斜面方向的分速度下滑,接着在 轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取
轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取 ="10" m/s2,sin37°=0.6,cos37°=0.8。求:
="10" m/s2,sin37°=0.6,cos37°=0.8。求:
(1)运动员从 点水平飞出时的速度大小
点水平飞出时的速度大小 ;
;
(2)运动员在 上着陆时,沿斜面方向的分速度大小
上着陆时,沿斜面方向的分速度大小 ;
;
(3)设运动员第一次和第四次滑上 轨道时上升的最大高度分别为
轨道时上升的最大高度分别为 和
和 ,则
,则 等于多少?
等于多少?
小车托着穿过打点计时器的纸带做匀变速直线运动,如图是经打点计时器打出的纸带的一段,计数点序号(按打点顺序计数)是A、B、C、D…….,以已知交流电的频率为50Hz,纸带上每相邻两个计数点间还有四个计时点。则小车的加速度大小是______ ,小车做_______运动(填“匀速”、“匀加速”或“匀减速”)。当打点计时器打A点时,小车速度为_______m/s(保留三位有效数字)
,小车做_______运动(填“匀速”、“匀加速”或“匀减速”)。当打点计时器打A点时,小车速度为_______m/s(保留三位有效数字) 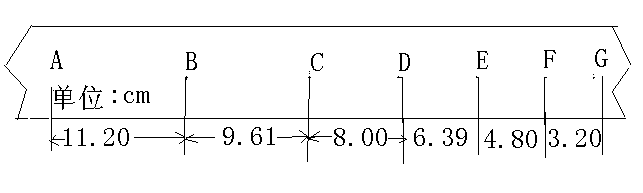
(本题10分)如图所示,一质量m=2kg的木块静止于水平地面上。现对物体施加一大小为10N的水平方向拉力。
(1)若地面光滑,求物体运动的加速度大小;
(2)若物体与地面间动摩擦因数μ=0.1,求物体的加速度大小和经过2s物体的位移大小。 (g=10 m/s2)
(本题10分)飞机着陆后匀减速滑行,它滑行的初速度是60m/s,加速度大小是3m/s2,则:(1)飞机着陆后滑行的时间是多少?(2)要滑行多远才能停下来?
如图所示,质量为m =10kg的物体,在F=60N水平向右的拉力作用下,由静止开始运动。设物体与水平面之间的动摩擦因素µ=0.4,g=10m/s2求:
(1)物体所滑动受摩擦力为多大?(2)在拉力的作用下物体运动的加速度为多大?
右图表示的是一个在细绳的结点O上悬挂重物的装置,细绳AO和BO的A、B端都是固定的。平衡时AO是水平的,BO与竖直方向的夹角为θ。若已知重物的重力为mg,求: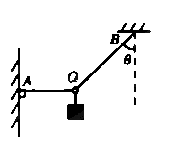
(1)AO的拉力F1的大小;
(2)BO的拉力F2的大小。