(本小题满分10分)已知函数，当点(x，y)是函数yf(x)-优题课

(本小题满分10分)
已知函数，当点(x，y) 是函数y = f (x) 图象上的点时，点是函数y = g(x) 图象上的点．
(1)   写出函数y = g (x) 的表达式；
(2)   当g(x)-f (x)0时，求x的取值范围；
(3)   当x在(2) 所给范围内取值时，求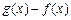的最大值．

科目数学题型解答题难度较易

已知函数 $f (x) = 2 \sin \frac{π}{4} \cos \frac{π}{4} + \sqrt{3} \cos \frac{π}{2}$ ．
（Ⅰ）求函数 $f (x)$ 的最小正周期及最值；
（Ⅱ）令 $g (x) = f (x + \frac{π}{3})$ ，判断函数 $g (x)$ 的奇偶性，并说明理由．

设函数 $f (x) = a x^{3} + b x^{2} - 3 a^{2} x + 1$ $(a, b \in R)$ 在 $x = x_{1}$ ， $x = x_{2}$ 处取得极值，且 $|x_{1} - x_{2}| = 2$ ．
（Ⅰ）若 $a = 1$ ，求 $b$ 的值，并求 $f (x)$ 的单调区间；
（Ⅱ）若 $a > 0$ ，求 $b$ 的取值范围．

在平面直角坐标系 $x o y$ 中，点 $P$ 到两点 $(0, \sqrt{3})$ ， $(0, - \sqrt{3})$ 的距离之和等于4，设点 $P$ 的轨迹为 $C$ ．
（Ⅰ）写出 $C$ 的方程；
（Ⅱ）设直线 $y = k x - 1$ 与 $C$ 交于 $A$ ， $B$ 两点． $k$ 为何值时 $\underset{O A}{\to}$ $⊥$ $\underset{O B}{\to}$ ？此时 $|\underset{A B}{\to}|$ 的值是多少？

数列 $|a_{n}|$ ， $|b_{n}|$ 是各项均为正数的等比数列，设 $c_{n} = \frac{b_{n}}{a_{n}} (n \in N^{*})$ ．

（Ⅰ）数列 $|c_{n}|$ 是否为等比数列？证明你的结论；

（Ⅱ）设数列 $|\ln a_{n}|, |\ln b_{n}|$ 的前 $n$ 项和分别为 $S_{n}, T_{n}$ ．若 $a_{1} = 2, \frac{S_{n}}{T_{n}} = \frac{n}{2 n + 1}$ ，求数列 $|c_{n}|$ 的前 $n$ 项和．

如图，在棱长为1的正方体 $A B C D - A^{`} B^{`} C^{`} {D^{`}}_{}$ 中， $A P = B Q = b (0 < b < 1)$ ，截面 $P Q E F ∥ A^{`} D$ ．

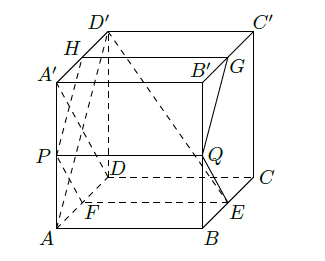
（Ⅰ）证明：平面 $P Q E F$ 和平面 $P Q G H$ 互相垂直；
（Ⅱ）证明：截面 $P Q E F$ 和截面 $P Q G H$ 面积之和是定值，
并求出这个值；
（Ⅲ）若 $b = \frac{1}{2}$ ，求 $D^{`} E$ 与平面 $P Q E F$ 所成角的正弦值．

试卷网试题网古诗词网作文网范文网