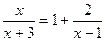(满分10分)如图,等边△ABC内接于⊙O,P是  上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交的延长线于
上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交的延长线于  点M.
点M.
(1)填空:∠APC=______度,∠BPC=_______度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求梯形PBCM的面积. 
(满分10分)已知关于 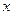 的方程
的方程 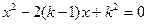 有两个实数根
有两个实数根  .
.
(1)求  的取值范围;
的取值范围;
(2)若 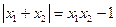 ,求
,求 
 的值;
的值;
(满分8分)近几年孝感市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级  名学生的升学意向,并根据调查结果绘制出如下两幅不完整的统计图.请你根据图中的信息解答下列问题:
名学生的升学意向,并根据调查结果绘制出如下两幅不完整的统计图.请你根据图中的信息解答下列问题:
(1)  ________;
________;
(2)扇形统计图中"职高"对应的扇形的圆心角  _________;
_________;
(3)请补全条形统计图;
(4)若该校九年级有学生900人,估计该校共有多少名毕业生的升学意向是职高? 
(满分8分)如图所示,网格中每个小正方形的边长为1,请你认真观察图(1)中的三个网格中阴影部分构成的图案,解答下列问题: 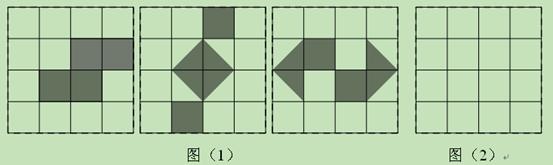
(1)这三个图案都具有以下共同特征:都是______对称图形,都不是____对称图形.
(2)请在图(2)中设计出一个面积为4,且具备上述特征的图案,要求所画图案不能与图(1)中所给出的图案相同.
(满分6分)解关于的方程: