图示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0.
(l)中央恒星O的质量是多大?
(2)经长期观测发现,A行星的实际运行轨道与理论轨道有少许偏差,并且每隔t0时间其运行轨道偏离理论轨道最大,天文学家认为出现这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行的圆轨道与A在同一平面内,且与A的绕行方向相同).根据上述现象和假设,试估算未知行星的运动周期和轨道半径.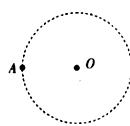
如图所示,距离为L的两块平行金属板A、B竖直固定在表面光滑的绝缘小车上,并与车内电动势为U的电池两极相连,金属板B下开有小孔,整个装置质量为M,静止放在光滑水平面上,一个质量为m带正电q的小球以初速度v0沿垂直于金属板的方向射入小孔,若小球始终未与A板相碰,且小球不影响金属板间的电场.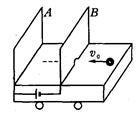
(1)当小球在A、 B板之间运动时,车和小球各做什么运动?加速度各是多少?
(2)假设小球经过小孔时系统电势能为零,则系统电势能的最大值是多少?从小球刚进入小孔,到系统电势能最大时,小车和小球相对于地面的位移各是多少?
如图所示,热电子由阴极飞出时的初速忽略不计,电子发射装置的加速电压为U0。电容器板长和板间距离均为L=10cm,下极板接地。电容器右端到荧光屏的距离也是L=10cm。在电容器两极板间接一交变电压,上极板的电势随时间变化的图像如左图,电势最大值Um=3U0。(假定每个电子穿过平行板的时间极短,可以认为电压是不变的)求:在t=0.06s时刻进入电容器的电子打在荧光屏上离O点的距离?
如图所示,一簇平行线为方向未知的匀强电场的电场线,沿与此平行线成60°角的方向,把一带电荷量为q= -2.0×10-6C的质点从A点移到B点,电场力做功为6.0×10-6J,已知A、B两点间距L=2cm。求匀强电场强度的大小并在图中注明其方向。
如图所示,两平行金属板A、B长i=8 cm,两板间距离d=8 cm,A板比B板电势高300 V,即UAB=300 V.一带正电的粒子电量q=10-10C,质量m=10-20kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106 m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在中心线上的O点的点电荷Q形成的电场区域(设界面PS右边点电荷的电场分布不受界面的影响).已知两界面MN、PS相距为L=12 cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏EF上.不计粒子重力。(静电力常数k=9×109 N·m2/C2)求: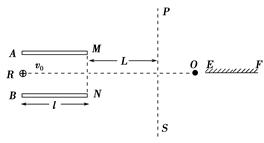
(1)粒子穿过界面PS时偏离中心线RO的距离多远;
(2)粒子从电场中飞出时的速度方向与水平方向的夹角θ;
(3)点电荷的电量.
如图所示,空间存在着强度E= 方向竖直向上的匀强电场,在电场内一长为
方向竖直向上的匀强电场,在电场内一长为 的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
(1)小球运动最高点时的速度;
(2)细线能承受的最大拉力;