某单位需以“挂号信”或“特殊快递”的方式向五所学校各寄一封信.这五封信的质量分别是90g,72g,215g,340g,400g. 根据这五所学校的地址及信件的质量范围,在邮局查得相关邮费标准如下:
| 业务种类 |
计费单位 |
资费标准 (元) |
挂号费 (元/封) |
特制信封 (元/个) |
| 挂号信 |
首重100g内,每20g |
0.8 |
3.0 |
0.5 |
| 续重101g—2000g 每100g |
2.0 |
|||
| 特快专递 |
首重1000g (含1000g) |
5.0 |
3.0 |
1.0 |
|
如图,在△ABC中, ,
, ,D为AC延长线上一点,
,D为AC延长线上一点, .过点D作
.过点D作 //
// ,交
,交 的延长线于点H.
的延长线于点H.
(1)求 的值;
的值;
(2)若 ,求AB的长.
,求AB的长.
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高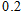 米,且AC=
米,且AC=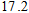 米,设太阳光线与水平地面的夹角为
米,设太阳光线与水平地面的夹角为 .当
.当 时,测得楼房在地面上的影长AE=
时,测得楼房在地面上的影长AE= 米,现有一只小猫睡在台阶的MN这层上晒太阳.(
米,现有一只小猫睡在台阶的MN这层上晒太阳.( 取
取 )
)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当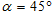 时,问小猫能否还晒到太阳?请说明理由.
时,问小猫能否还晒到太阳?请说明理由.
已知:如图,AB∥CD,E是AB的中点,CE=DE.
求证:(1)∠AEC=∠BED;(2)AC=BD.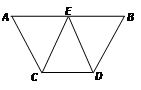
如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)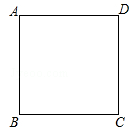
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1,60)