如图,正方形 所在平面与圆
所在平面与圆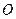 所在平面相交于
所在平面相交于 ,线段
,线段 为圆
为圆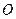 的弦,
的弦,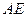 垂直于圆
垂直于圆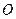 所在平面,垂足
所在平面,垂足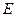 是圆
是圆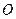 上异于
上异于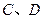 的点,
的点, ,圆
,圆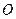 的直径为
的直径为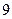 ,
,
1)求证:平面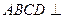 平面
平面 2)求二面角
2)求二面角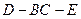 的平面角的正切值.
的平面角的正切值.
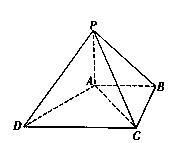
如图,四棱锥 中,
中,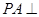 底面
底面 ,
, ,底面
,底面 为梯形,
为梯形, ,
, ,
, .
.
(1)求证:平面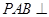 平面
平面 ;
;
(2)求四棱锥 的体积
的体积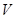 .
.
某班为了调查同学们周末的运动时间,随机对该班级50名同学进行了不记名的问卷调查,得到了如下表所示的统计结果:
| 运动时间不超过2小时 |
运动时间超过2小时 |
合计 |
|
| 男生 |
10 |
20 |
30 |
| 女生 |
13 |
7 |
20 |
| 合计 |
23 |
27 |
50 |
(1)根据统计结果,能否在犯错误概率不超过0.05的前提下,认为该班同学周末的运动时间与性别有关?
(2)用分层抽样的方法,从男生中抽取6名同学,再从这6名同学中随机抽取2名同学,求这两名同学中恰有一位同学运动时间超过2小时的概率.
附: ,其中
,其中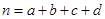 .
.
设函数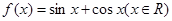 .
.
(1)求函数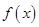 的最小正周期和最值;
的最小正周期和最值;
(2)若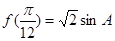 ,其中A是面积为
,其中A是面积为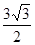 的锐角
的锐角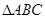 的内角,且
的内角,且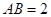 ,求边
,求边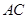 和
和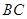 的长.
的长.
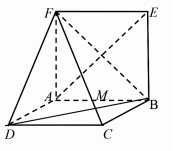
矩形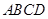 与矩形
与矩形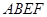 的公共边为
的公共边为 ,且平面
,且平面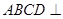 平面
平面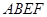 ,如图所示,
,如图所示, ,
,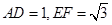 .
.
(1)证明: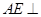 平面
平面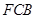 ;
;
(2)求异面直线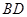 与
与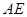 所成角的余弦值;
所成角的余弦值;
(3)若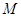 是棱
是棱 的中点,在线段
的中点,在线段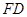 上是否存在一点
上是否存在一点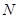 ,使得
,使得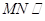 平面
平面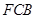 ?证明你的结论.
?证明你的结论.
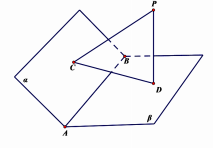
如图,已知二面角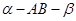 的大小为
的大小为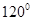 ,
,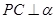 于C,
于C,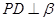 于
于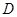 ,且
,且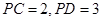 .
.
(1)求异面直线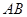 与
与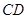 所成角的大小;
所成角的大小;
(2)求点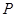 到直线
到直线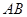 的距离.
的距离.