2005年10月17日,我国第二艘载人飞船“神州六号”,在经过了115个小时32分钟的太空飞行后顺利返回。
(1)飞船在竖直发射升空的加速过程中,宇航员处于超重状态。设点火后不久,仪器显示宇航员对座舱的压力等于他体重的4倍,求此时飞船的加速度大小。地面附近重力加速度g = 10m/s2。
(2)飞船变轨后沿圆形轨道环绕地球运行,运行周期为T。已知地球半径为R,地球表面的重力加速度为g。求飞船离地面的高度。
如图示 ,光滑水平地面上放有一质量为m的导热气缸,用活塞封闭了一部分气体。活塞质量为m/2 ,截面积为S,可无摩擦滑动,气缸静止时与缸底距离为L0。现用水平恒力F 向右推气缸,最后气缸与活塞达到相对静止状态。已知大气压强为P0 .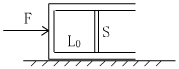
求(1)稳定时封闭气体的压强
(2)稳定时活塞与缸底部的距离?
如图,两根劲度系数分别为K1、K2的轻质弹簧与小球相连结,另外一端固定不动。整个装置位于光滑的水平地面上。当小球位于O点时,两弹簧均处于原长状态。今把小球沿弹簧轴线方向拉离O一小段距离后放手。证明小球此后的运动为简谐运动。
某仪器用电场和磁场来控制电子在材料表面上方的运动,如图所示,材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场,电场宽为d;矩形区域NN′M′M充满垂直纸面向里的匀强磁场,磁感应强度为B,长为3s,宽为s;NN′为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子,从P点开始被电场加速经隔离层垂直进入磁场,电子每次穿越隔离层,时间极短、运动方向不变,其动能损失是每次穿越前动能的10%,最后电子仅能从磁场边界M′N′飞出。不计电子所受重力。
(1)控制电子在材料表面上方运动,最大的电场强度为多少?
(2)若电子以上述最大电场加速,经多长时间将第三次穿越隔离层?
(3)A是M′N′的中点,若要使电子在A、M′间垂直于AM′飞出,求电子在磁场区域中运动的时间。
如图所示,一对半径均为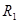 的金属板M、N圆心正对平行放置,两板距离为
的金属板M、N圆心正对平行放置,两板距离为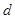 ,N板中心镀有一层半径为
,N板中心镀有一层半径为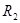 的圆形锌金属薄膜,
的圆形锌金属薄膜,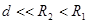 ,两板之间电压为
,两板之间电压为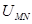 ,两板之间真空且可视为匀强电场。N板受到某种单色光照射后锌金属薄膜表面会发射出最大速率为
,两板之间真空且可视为匀强电场。N板受到某种单色光照射后锌金属薄膜表面会发射出最大速率为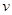 ,方向各异的电子,已知电子的电荷量为
,方向各异的电子,已知电子的电荷量为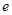 ,质量为
,质量为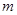 ,每秒稳定发射
,每秒稳定发射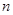 个电子。电子在板间运动过程中无碰撞且不计电子的重力和电子间相互作用,电子到达M板全部被吸收。M板右侧串联的电流表可以测量到通过M板的电流
个电子。电子在板间运动过程中无碰撞且不计电子的重力和电子间相互作用,电子到达M板全部被吸收。M板右侧串联的电流表可以测量到通过M板的电流 。试求:
。试求:
(1)当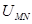 取什么值时,
取什么值时, 始终为零;
始终为零;
(2)当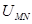 取什么值时,
取什么值时, 存在一个最大值,并求这个最大值;
存在一个最大值,并求这个最大值;
(3)请利用(1)(2)的结论定性画出 随
随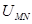 变化的图像。
变化的图像。
飞机若仅依靠自身喷气式发动机推力起飞需要较长的跑道,某同学设计在航空母舰上安装电磁弹射器以缩短飞机起飞距离,他的设计思想如下:如图所示,航空母舰的水平跑道总长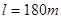 ,其中电磁弹射器是一种长度为
,其中电磁弹射器是一种长度为 的直线电机,这种直线电机从头至尾可以提供一个恒定的牵引力
的直线电机,这种直线电机从头至尾可以提供一个恒定的牵引力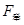 。一架质量为
。一架质量为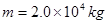 的飞机,其喷气式发动机可以提供恒定的推力
的飞机,其喷气式发动机可以提供恒定的推力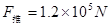 。考虑到飞机在起飞过程中受到的阻力与速度大小有关,假设在电磁弹射阶段的平均阻力为飞机重力的0.05倍,在后一阶段的平均阻力为飞机重力的0.2倍。飞机离舰起飞的速度
。考虑到飞机在起飞过程中受到的阻力与速度大小有关,假设在电磁弹射阶段的平均阻力为飞机重力的0.05倍,在后一阶段的平均阻力为飞机重力的0.2倍。飞机离舰起飞的速度 ,航母处于静止状态,飞机可视为质量恒定的质点。请你求出(计算结果均保留两位有效数字)。
,航母处于静止状态,飞机可视为质量恒定的质点。请你求出(计算结果均保留两位有效数字)。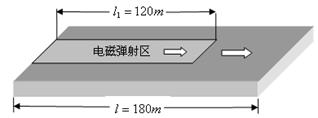
(1)飞机在后一阶段的加速度大小;
(2)电磁弹射器的牵引力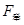 的大小;
的大小;
(3)电磁弹射器输出效率可以达到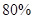 ,则每弹射这样一架飞机电磁弹射器需要消耗多少能量。
,则每弹射这样一架飞机电磁弹射器需要消耗多少能量。