(本小题满分12分)
在平面直角坐标系xOy中，抛物线的解析式是y =
+1，点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点P(t，0)在x轴上.
(1) 写出点M的坐标；
(2) 当四边形CMQP是以MQ，PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围；
② 当梯形CMQP的两底的长度之比为1：2时，求t的值.
如图，△
是等边三角形，点
、
分别是
、
的延长线上的点，且
，
的延长线交
于点
．
（1）求证：
；
（2）求
的度数．
如图，在等腰RT△
中，
，
，点
是斜边
的中点，点
、
分别为
、
边上的点，且
．
（1）判断
与
的大小关系，并说明理由；
（2）若
，
，求△
的面积．
．如图，在△ABC中，点E在AB上，点D在BC上，BD=BE，∠BAD=∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．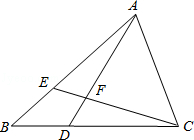
如图所示，一根旗杆升旗的绳垂直落地后还剩余1米，若将绳子拉直，则绳端离旗杆底端的距离（BC）有5米．求旗杆的高度．
如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′；
（2）在直线l上找一点P（在答题纸上图中标出），使PB+PC
的长最短，这个最短长度是 ．