已知点P的坐标为
,在
轴上存在点
(不与
点重合),以
为边作正方形
,使点
落在反比例函数
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点
在第四象限,另一个正方形的顶点
在第二象限.
(1)如图所示,若反比例函数解析式为
,
点坐标为
,图中已画出一符合条件的一个正方形
,请你在图中画出符合条件的另一个正方形
,并写出点
的坐标;

(温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!)
M1的坐标是 ▲
(2) 请你通过改变P点坐标,对直线M1 M的解析式
进行探究可得 k﹦
(3) 依据(2)的规律,如果点P的坐标为
,请你求出点M1和点M的坐标.
如图1,在四边形ABCD的AB边上任取一点E(点E不与点A、点B重合),分别连接ED、EC,可以把四边形ABCD分成3个三角形.如果其中有2个三角形相似,我们就把点E叫做四边形ABCD的AB边上的相似点;如果这3个三角形都相似,我们就把点E叫做四边形ABCD的AB边上的强相似点.
(1)若图1中,∠A=∠B=∠DEC=50°,说明点E是四边形ABCD的AB边上的相似点;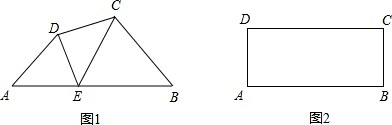
(2)①如图2,画出矩形ABCD的AB边上的一个强相似点.(要求:画图工具不限,不写画法,保留画图痕迹或有必要的说明.)
②对于任意的一个矩形,是否一定存在强相似点?如果一定存在,请说明理由;如果不一定存在,请举出反例.
(3)在梯形ABCD中,AD∥BC,AD<BC,∠B=90°,点E是梯形ABCD的AB边上的一个强相似点,判断AE与BE的数量关系并说明理由.
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E、与OB交于点F,连接CE、CF.
(1)AB与⊙O相切吗,为什么?
(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.
施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系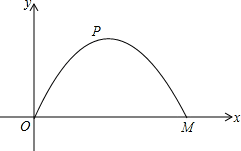
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明.
小林家、小华家与图书馆依次在一条直线上.小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书,已知小林到达图书馆花了20分钟.设两人出发x(分钟)后,小林离小华家的距离为y(米),y与x的函数关系如图所示.
(1)小林的速度为米/分钟,a=,小林家离图书馆的距离为米;
(2)已知小华的步行速度是40米/分钟,设小华步行时与家的距离为y1(米),请在图中画出y1(米)与x(分钟)的函数图象;
(3)小华出发几分钟后两人在途中相遇?
如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离BC为10m,测角仪的高度CD为1.5m,测得树顶A的仰角为33°.求树的高度AB.(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)