(本题8分)
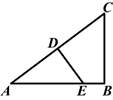
如图,AB是⊙O的直径,C是 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ▲ ,CE的长是 ▲ .
如图,若∠1=∠2,则图中有哪些三角形相似?分别把它们写出来,并说明理由.
如图,已知AB=1cm,BD=2cm,AC=2cm,CE=4cm,△ABC与△ADE是否相似?请说明理由.
下面给出△ABC和△DEF的各条边长,是否能判定△ABC∽△DEF?为什么?
(1)AB=3cm,BC=4cm,AC=5cm,DE=1.5cm,EF=2cm,DF=3cm;
(2)AB=4cm,BC=7cm,AC=5cm,DE=2cm,EF=3.5cm,DF=2.5cm;
(3)AB=8cm,BC=10cm,AC=9cm,DE=10cm,EF=25cm.DF=18cm.
如图所示,E是□ABCD的边BC延长线上的一点,连接AE,交边CD于点F.在不添加辅助线的情况下,图中相似的三角形有几对?请分别写出来,并说明判定的依据.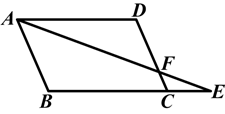
如图,△ADE∽△ABC,∠AED=∠C,分别找出△ADE的各边的对应边和各角的对应角,并写出对应边的比例式.