过山车是游乐场中常见的设施。下图是一种过山车的简易模型，它由水平轨道和在竖直平面内的三个圆形轨道组成，B、C、D分别是三个圆形轨道的最低点，B、C间距与C、D间距相等，半径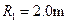
、
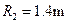。一个质量为
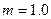kg的小球（视为质点），从轨道的左侧A点以
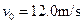的初速度沿轨道向右运动，A、B间距
m。小球与水平轨道间的动摩擦因数
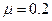，圆形轨道是光滑的。假设水平轨道足够长，圆形轨道间不相互重叠。重力加速度取
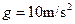，计算结果保留小数点后一位数字。试求
（1）小球在经过第一个圆形轨道的最高点时，轨道对小球作用力的大小；
（2）如果小球恰能通过第二圆形轨道，B、C间距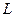
应是多少；
（3）在满足（2）的条件下，如果要使小球不能脱离轨道，在第三个圆形轨道的设计中，半径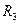
应满足的条件；小球最终停留点与起点
的距离。
一质点做匀加速直线运动，初速度为10m/s ，加速度为2m/s2 。试求该质点：第5s末的速度20 m/s
前5s内的平均速度15m/s
第5s内的平均速度19m/s
如图所示，一电荷量q=3×10-5C带正电的小球，用绝缘细线悬于竖直放置足够大的平行金属板中的O点。电键S合上后，当小球静止时，细线与竖直方向的夹角α=37°。已知两板相距d=0.1m，电源电动势
=15V，内阻r=0.5Ω，电阻R1=3Ω，R2=R3= R4 =8Ω。g取10m/s2，已知
，
。求：
17
电源的输出功率；
两板间的电场强度的大小；
带电小球的质量。
如图甲所示的电路中，R1、R2均为定值电阻，且R1＝100 Ω，R2阻值未知，R3为一滑动变阻器．当其滑片P从左端滑至右端时，测得电源的路端电压随电源中流过的电流变化图线如图乙所示，其中A、B两点是滑片P在变阻器的两个不同端点得到的．求：
电源的电动势和内阻.
定值电阻R2的阻值．
滑动变阻器的最大阻值．
如图所示，在两根劲度系数都为k的相同的轻质弹簧下悬挂有一根导体棒ab，导体棒置于水平方向的匀强磁场中，且与磁场垂直.磁场方向垂直纸面向里，当导体棒中通以自左向右的恒定电流时，两弹簧各伸长了Δl1；若只将电流反向而保持其他条件不变，则两弹簧各伸长了Δl2，求：
导体棒通电后受到的磁场力的大小?
若导体棒中无电流，则每根弹簧的伸长量为多少?
如图所示，电源电动势E＝6V，电源内阻不计．定值电阻R1=2.4kΩ、R2=4.8kΩ.
若在ab之间接一个C=100μF的电容器，闭合开关S，电路稳定后，求电容器上所带的电量；
若在ab之间接一个内阻RV = 4.8kΩ的电压表，求电压表的示数．