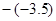如图,正比例函数 的图象与反比例函数
的图象与反比例函数
 在第一象限的图象交于
在第一象限的图象交于 点,过
点,过 点作
点作 轴的垂线,垂足为
轴的垂线,垂足为 ,已知
,已知 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 与点
与点 不重合),且
不重合),且 点的横坐标为1,在
点的横坐标为1,在 轴上求一点
轴上求一点 ,使
,使 最小.
最小.
某自行车厂计划一周生产1400辆自行车,平均每天生产200辆,由于各种原因,实际每天的生产量与计划量相比有出入。
下表是某周的生产情况(超产为正,减产为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
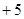 |
 |
 |
 |
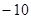 |
 |
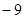 |
(1)根据记录可知前三天共生产了_________辆;
(2)产量最多的一天比产量最少的一天多生产__________辆;
(3)该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
甲说任何含字母的代数式的值,都随字母取值的变化而变化;乙说未必如此,还举了一个例子,说:不论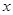 、
、 取任何有理数,多项式
取任何有理数,多项式 的值恒等于一个常数,你认为谁的说法正确?请说明理由。
的值恒等于一个常数,你认为谁的说法正确?请说明理由。
根据条件建立方程模型。
(1)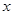 的5倍比它的2倍大3;
的5倍比它的2倍大3;
(2)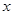 的
的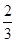 与4的差等于它的相反数;
与4的差等于它的相反数;
(3)某人买苹果5千克,付出10元,找回1元5角,设每千克苹果的价格为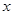 元。
元。
已知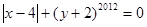 ,求
,求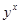 的值。
的值。
在数轴上标出下列各数,再用“<”连接起来。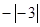 ,0,
,0,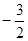 ,
,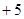 ,
,