如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．
(1)求证：AB＝DC；
(2)试判断△OEF的形状，并说明理由．
如图,直升飞机在资江大桥AB的上方P点处，此时飞机离地面的高度PO=450米，且A、B、O三点在一条直线上，测得大桥两端的俯角分别为α=30°，β=45°，求大桥的长AB．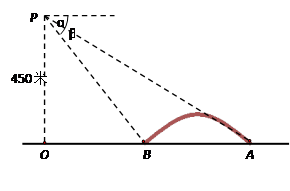
[
-
]·-6；
有一种足球是由若干块黑白相间的牛皮缝制而成的，黑皮可看作正五边形，白皮可看作正六边形.
（1）一只足球黑皮共有12块，比白皮块数的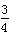
少3块，问白皮有多少块？
（2）我们看到每块白皮有三条边和黑皮连在一起，每块黑皮的五条边都和白皮连在一起. 已知黑白皮共有32块，你知道白皮和黑皮各有多少块吗？
同一直线上有A、B、C、D四点，已知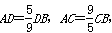
，且CD＝4cm，求AB的长.
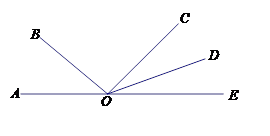
如图，点A、O、E在同一直线上，∠AOB＝40°，∠DOE＝28°，OD平分∠COE， 求∠COB的度数.