如图所示是一个设计“过山车”的试验装置的原理示意图,斜面AB与竖直面内的圆形轨道在B点平滑连接,圆形轨道半径为R。一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,A点距水平面的高度为4R,当它第一次经过B点进入圆形轨道时对轨道的压力为其重力的7倍,小车恰能完成圆周运动并第二次经过最低点B后沿水平轨道向右运动。已知重力加速度为g,斜面轨道与底面的夹角为530。(sin530="0.8 " cos530=0.6)求:
(1)小车第一次经过B点时的速度大小vB;
(2)小车在斜面轨道上所受阻力与其重力之比k;
(3)假设小车在竖直圆轨道左、右半圆轨道部分克服阻力做的功相等,求小车第二次经过竖直圆轨道最低点时的速度大小 ?
?
一摩托车由静止开始在平直的公路上行驶,其运动过程的v-t图像如图所示,求: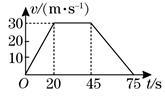
(1)摩托车在0-20s这段时间的加速度大小a;
(2)摩托车在0-75s这段时间的平均速度大小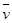 。
。
如图甲所示,水平面上的两光滑金属导轨平行固定放置,间距d=0.5 m,电阻不计,左端通过导线与阻值R=2 Ω的电阻连接,右端通过导线与阻值RL=4 Ω的小灯泡L连接。在CDFE矩形区域内有竖直向上的匀强磁场,CE长l=2 m,有一阻值r=2 Ω的金属棒PQ放置在靠近磁场边界CD处(恰好不在磁场中)。CDFE区域内磁场的磁感应强度B随时间变化如图乙所示。在t=0至t=4 s 内,金属棒PQ保持静止,在t=4 s时使金属棒PQ以某一速度进入磁场区域并保持匀速运动。已知从t=0开始到金属棒运动到磁场边界EF处的整个过程中,小灯泡的亮度没有发生变化。求: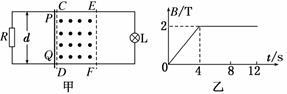
(1)通过小灯泡的电流;
(2)金属棒PQ在磁场区域中运动的速度大小。
如图所示,水平放置的两块长直平行金属板a、b相距d =0.10 m,a、b间的电场强度为E=5.0×105 N/C,b板下方整个空间存在着磁感应强度大小为B=0.6 T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25 kg、电荷量为q=1.6×10-18 C的带正电的粒子(不计重力),从贴近a板的左端以v0=1.0×106 m/s的初速度水平射入匀强电场,刚好从狭缝P处穿过b板而垂直进入匀强磁场,最后粒子回到b板的Q处(图中未画出).求: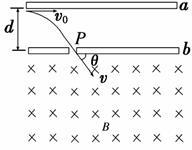
(1)判断a、b两板间电场强度的方向;
(2)求粒子到达P处的速度与水平方向的夹角θ;
(3)求P、Q之间的距离L(结果可保留根号).
空间有一半径为R的圆形匀强磁场区域,磁场方向垂直于纸面.一质量为m、电荷量为q(q>0)的粒子以速率v0从A点沿圆的半径AO射入磁场,从B点沿半径OB方向离开磁场,形成如图所示的轨迹,已知∠AOB=θ=120°,不计粒子的重力。求: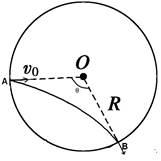
(1)该圆形区域内匀强磁场的磁感应强度大小和方向,
(2)该粒子从A运动到B的时间。
如图所示,足够长的平行光滑金属导轨水平放置,宽度L="0.4" m,一端连接R=1Ω的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度B=1T。把电阻r=1Ω的导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。导轨的电阻可忽略不计。在平行于导轨的拉力F作用下,导体棒沿导轨向右匀速运动,速度v="5" m/s。求:
(1)感应电流I和导体棒两端的电压U;
(2)拉力F的大小;
(3)拉力F的功率
(4)电路中产生的热功率