国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价 (万元)之间满足关系式
(万元)之间满足关系式 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本 (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
(1)直接写出 与x之间的函数关系式;
与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
如图,已知等边三角形ABC,以边BC为直径的半圆与边AB、AC分别交于点D、点E,过点E作EF⊥AB,垂足为点F.
(1)判断EF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若等边△ABC的边长为8,求FH的长.(结果保留根号)
如图,某同学在楼房的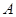 处测得荷塘的一端
处测得荷塘的一端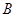 处的俯角为
处的俯角为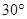 ,荷塘另一端
,荷塘另一端 处
处 、
、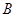 在同一条直线上,已知
在同一条直线上,已知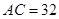 米,
米, 米,求荷塘宽
米,求荷塘宽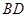 为多少米?(结果保留根号)
为多少米?(结果保留根号)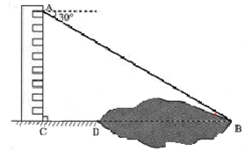
在直角坐标平面内,二次函数图象的顶点为 ,且过点
,且过点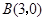 .
.
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与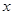 轴的另一个交点的坐标.
轴的另一个交点的坐标.
如图,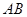 是⊙O的一条弦,
是⊙O的一条弦,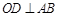 ,垂足为
,垂足为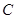 ,交⊙O于点
,交⊙O于点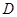 ,点
,点 在⊙O上.
在⊙O上.
(1)若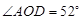 ,求
,求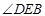 的度数;
的度数;
(2)若 ,
, ,求
,求 的长.
的长.
如图,在平行四边形ABCD中,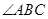 的平分线
的平分线 分别与
分别与 、
、 交于点
交于点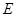 、
、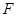 .
.
(1)求证: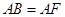 ;
;
(2)当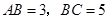 时,求
时,求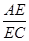 的值.
的值.