(本小题满分14分)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交椭圆于A、B两个不同点。
交椭圆于A、B两个不同点。
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形。 
在直角坐标系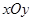 中,直线
中,直线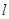 的参数方程为
的参数方程为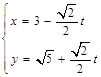 (
(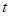 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系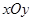 取相同的长度单位,且以原点
取相同的长度单位,且以原点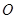 为极点,以
为极点,以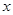 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆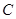 的方程为
的方程为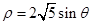 。
。
(1)求圆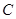 的直角坐标方程;
的直角坐标方程;
(2)设圆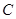 与直线
与直线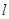 交于点
交于点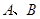 。若点
。若点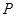 的坐标为(3,
的坐标为(3,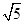 ),求
),求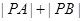 。
。
求函数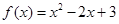 在下列定义域内的值域。
在下列定义域内的值域。
(1)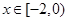 函数y=f(x)的值域
函数y=f(x)的值域
(2)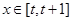 (其中
(其中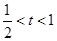 )函数y=f(x)的值域。
)函数y=f(x)的值域。
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},
C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若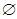
 A∩B,A∩C=
A∩B,A∩C=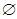 ,求a的值.
,求a的值.
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
设函数f(x)=(1+x)2-2ln (1+x).
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=x2+x+a在[0,2]上恰有两个相异实根,求实数a的取值范围.