如图，将OA = 6，AB = 4的矩形OABC放置在平面直角坐标系中，动点M、N以每秒１个单位的速度分别从点A、C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交OB于点P，连接MP．
（1）点B的坐标为 ；用含t的式子表示点P的坐标为 ；(3分)
（2）记△OMP的面积为S，求S与t的函数关系式（0 < t < 6）；并求t为何值时，S有最大值？(4分)
（3）试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC面积的
？若存在，求出点T的坐标；若不存在，请说明理由．(3分)
如图，某居民小区内
两楼之间的距离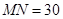
米，两楼的高都是20米，
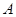楼在
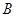楼正南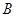，楼窗户朝南。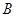楼内一楼住户的窗台离小区地面的距离
米，窗户高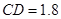
米。当正午时刻太阳光线与地面成
角时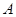，楼的影子是否影响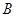楼的一楼住户采光？若影响，挡住该住户窗户多高？若不影响，请说明理由。（参考数据：
，
，
）
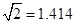如图，AC为⊙O的直径，AC=4，B、D分别在AC两侧的圆上，∠BAD=60°，BD与AC的交点为E．
（1）求点O到BD的距离及∠OBD的度数；
（2）若DE=2BE，求
的值和CD的长．
如图，在□ABCD中，AB＝5，AD＝10，cosB＝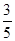
，过BC的中点E作EF⊥AB，垂足为点F，连结DF，求DF的长．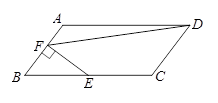
解方程组：
已知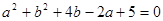
，求
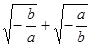的值。