为了研究太阳演化进程,需知道目前太阳的质量M。已知地球半径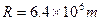 ,地球质量
,地球质量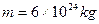 ,日地中心距离
,日地中心距离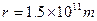 ,地球表面处的重力加速度
,地球表面处的重力加速度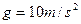 ,地球绕太阳一周所用的时间1年约为
,地球绕太阳一周所用的时间1年约为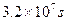 ,试估算目前太阳的质量M(保留一位有效数字,引力常量未知)
,试估算目前太阳的质量M(保留一位有效数字,引力常量未知)
如图甲所示,在光滑绝缘的水平桌面上建立一xoy坐标系,平面处在周期性变化的电场和磁场中,电场和磁场的变化规律如图乙所示(规定沿+y方向为电场强度的正方向,竖直向下为磁感应强度的正方向).在t=0时刻,一质量为m=10g、电荷量为q=0.1C的带电金属小球自坐标原点O处,以v0=2m/s的速度沿x轴正方向射出.已知E0=0.2N/C、B0=0.2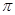 T.求:
T.求: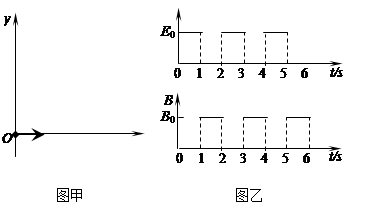
(1)t=1s末速度的大小和方向;
(2)1s~2s内,金属小球在磁场中做圆周运动的半径和周期;
(3)试求出第3秒末小球所在位置的坐标。
如图,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为θ=300的光滑斜面连接,质量m=1.0kg的小滑块从圆弧顶点D由静止释放,已知滑块与水平面间的动摩擦因数μ=0.1.,取g=10m/s2.求: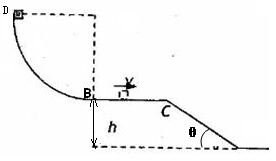
(1)小滑块刚到达圆弧的B点时对圆弧的压力;
(2)小滑块到达C点时速度的大小;
(3)小滑块从C点运动到地面所需的时间。
为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接,如图所示。一个小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数u=0.50(g取10m/s2,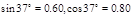 )求:
)求: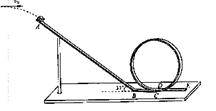
(1)小物块的抛出点和A点的高度差;
(2)要使小物块不离开轨道,并从水平轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件;
(3)为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件。
《愤怒的小鸟》是一款时下非常流行的游戏,故事也相当有趣,如图甲,为了报复偷走鸟蛋的肥猪们,鸟儿以自己的身体为武器,如炮弹般弹射出去攻击肥猪们的堡垒.某班的同学们根据自己所学的物理知识进行假设:小鸟被弹弓沿水平方向弹出,如图乙所示,其中h1=0.8m,l1=2m,h2=2.4m,l2=1m,请回答下面两位同学提出的问题(取g=10m/s2):
(1)A同学问:如图乙所示,小鸟以多大速度水平弹出刚好擦着台面草地边缘落在地面上?
(2)B同学问:如图乙所示,小鸟飞出能否直接打中肥猪?请用计算结果进行说明.
在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(取g=10m/s2)。求:
(1)小球在最高点不脱离轨道的最小速率是多少?
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是多少?