如图，过A（8，0）、B（0，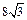
）两点的直线与直线
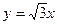交于点C．平行于
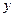轴的直线
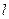从原点O出发，以每秒1个单位长度的速度沿
轴向右平移，到C点时停止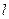；分别交线段BC、OC于点D、E，以DE为边向左侧作等边△
DEF，设△DEF与△BCO重叠部分的面积为S（平方单位），直线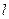的运动时间为t（
秒）．
（1）直接写出C点坐标和t的取值范围；
（2）求S与t的函数关系式；
（3）设直线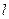与轴交于点P，是否存在这样的点P，使得以P、O、F为顶点的三角形为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．
以直线
为对称轴的抛物线过点A（3，0）和点B(0，3)，求此抛物线的解析式.
如图：已知，梯形ABCD中，∠B=90°，AD∥BC，AB⊥BC，AB=AD=3，BC=
7.
求cos∠C.
已知抛物线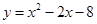
.（1）用配方法把
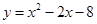化为
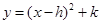形式；（2）并指出：抛物线的顶点坐标是，抛物线的对称轴方程是，
抛物线与x轴交点坐标是，当x时，y随x的增大而增大.
解
( 本题12分) 已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E。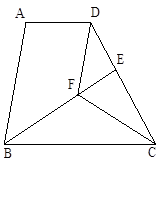
求证：（1）△BFC≌△DFC；
（2）AD=DE
( 本题10分) 某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：
| 运输工具 |
运输费单价 （元/吨·千米） |
冷藏费单价 （元/吨·小时） |
过路费 （元） |
装卸及管理费 （元） |
| 汽车 |
2 |
5 |
200 |
0 |
| 火车 |
1.8 |
5 |
0 |
1600 |
注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨·小时”表示每吨货物每小时的冷藏费．（1）设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y1（元）和y2（元），试求出y1和y2和与x的函数关系式；
（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？