希腊数学家丢番图(公元3~4世纪)的墓碑上记载着: “他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两颊长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他有了儿子,感到很幸福;可是,儿子只活了他父亲全部生命的一半;儿子死后,他又在极度的悲伤中度过了四年,也与世长辞了.”
根据以上的信息,请你计算出:
(1)丢番图死时多少岁?
(2)丢番图结婚时多少岁?
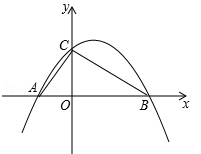
(宜宾)如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(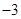 ,
,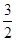 ),AB=1,AD=2.
),AB=1,AD=2.
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数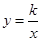 (
(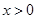 )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.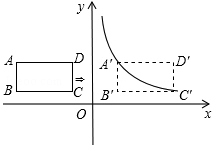
(宜宾)如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.
(1)求证:直线BC是⊙O的切线;
(2)若AE=2,tan∠DEO=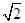 ,求AO的长.
,求AO的长.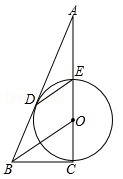
(宜宾)如图,抛物线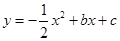 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.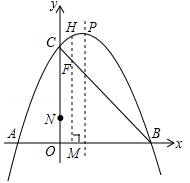
(遂宁)如图,AB为⊙O的直径,直线CD切⊙O于点D,AM⊥CD于点M,BN⊥CD于N.
(1)求证:∠ADC=∠ABD;
(2)求证:AD2=AM•AB;
(3)若AM= ,sin∠ABD=
,sin∠ABD=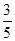 ,求线段BN的长.
,求线段BN的长.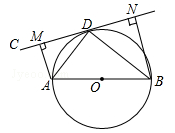
(遂宁)如图,已知抛物线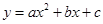 经过A(﹣2,0),B(4,0),C(0,3)三点.
经过A(﹣2,0),B(4,0),C(0,3)三点.
(1)求该抛物线的解析式;
(2)在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;
(3)若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.