理论证明：卫星围绕中心天体以速度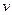
做匀速圆周运动时，如果将卫星速度突然增大到
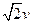，卫星就可以摆脱中心天体的引力。由于万有引力和点电荷之间的库仑力均与距离平方成反比，所以，电子围绕原子核的运动与卫星的运动是相似的。有一质量为
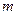、电量为-
的电子围绕电量为Q的原子核在半径为
的圆周上做匀速圆周运动，受到光的照射，电子吸收能量从而脱离原子核的吸引。回答下列问题：
（1）电子绕原子核在半径为的圆周上做匀速圆周运动的速度是多大？
( 2 ) 电子绕原子核在半径为的圆周上做匀速圆周运动的周期是多大？
（3）电子至少吸收多大能量才能脱离原子核的吸引？
在xoy平面内，直线OP与y轴的夹角
=45o。第一、第二象限内存在大小相等，方向分别为竖直向下和水平向右的匀强电场,电场强度E=1.0×105N/C ；在x轴下方有垂直于纸面向外的匀强磁场，磁感应强度B=0.1T，如图所示。现有一带正电的粒子从直线OP上某点A（-L, L）处静止释放。设粒子的比荷
，粒子重力不计。求：
（1）当L=2cm时，粒子进入磁场时与x轴交点的横坐标
（2）当L=2cm时，粒子进入磁场时速度的大小和方向
（3）如果在直线OP上各点释放许多个上述带电粒子（粒子间的相互作用力不计），试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线（提示：写出圆心点坐标x、y的函数关系）
2012年我们中国有了自己的航空母舰“辽宁号”，航空母舰上舰载机的起飞问题一直备受关注。某学习小组的同学对舰载机的起飞进行了模拟设计。如图，舰载机总质量为m，发动机额定功率为P，在水平轨道运行阶段所受阻力恒为f。舰载机在A处启动，同时开启电磁弹射系统，它能额外给舰载机提供水平方向推力，经历时间t1，舰载机匀加速运行至B处，速度达到v1，电磁弹射系统关闭。舰载机然后以额定功率加速运行至C处，经历的时间为t2，速度达到v2。此后，舰载机进入倾斜曲面轨道，在D处离开航母起飞。求
（1）AB间距离；
（2）舰载机在AB间运动时获得的总动力；
（3）BC间距离。
如图，顶角为90°的“∨”型光滑金属导轨MON固定在倾角为θ的绝缘斜面上，M、N连线平行于斜面底端，导轨MO、NO的长度相等，M、N两点间的距离L＝2m，整个装置处于磁感应强度大小B＝0.5T、方向垂直于斜面向下的匀强磁场中。一根质量m=0.4kg,粗细均匀、单位长度电阻值r＝0.5Ω/m的导体棒ab，受到平行于斜面向上且垂直于ab的变力F作用，以速度v＝2m/s沿导轨向下匀速滑动，导体棒在运动过程中始终与导轨接触良好，不计导轨电阻，从导体棒在MN时开始计时，
⑴t=0时，F=0，求斜面倾角θ；
⑵求0.2s内通过导体棒的电荷量q；
⑶求导体棒通过整个金属导轨的过程中产生的焦耳热Q。
如图所示，在水平光滑轨道PQ上有一个轻弹簧，其左端固定，现用一质量m＝2.0 kg的小物块(视为质点)将弹簧压缩后释放，物块离开弹簧后经过水平轨道右端恰好沿半圆轨道的切线进入竖直固定的轨道，小物块进入半圆轨道后恰好能沿轨道运动，经过最低点后滑上质量M＝8.0 kg的长木板，最后恰好停在长木板最左端．已知竖直半圆轨道光滑且半径R＝0.5 m，物块与木板间的动摩擦因数μ＝0.2，木板与水平地面间摩擦不计，取g＝10 m/s2.求：
(1)弹簧具有的弹性势能；
(2)小物块滑到半圆轨道底端时对轨道的压力大小 ；
(3)木板的长度．
如图所示，一质量为m、电量为+q、重力不计的带电粒子，从A板的S点由静止开始释放，经A、B加速电场加速后，穿过中间偏转电场，再进入右侧匀强磁场区域．已知AB间的电压为U，MN极板间的电压为2U，MN两板间的距离和板长均为L，磁场垂直纸面向里、磁感应强度为B、有理想边界．求：
（1）带电粒子离开B板时速度v0的大小；
（2）带电粒子离开偏转电场时速度v的大小与方向；
（3）要使带电粒子最终垂直磁场右边界射出磁场，磁场的宽度d多大？